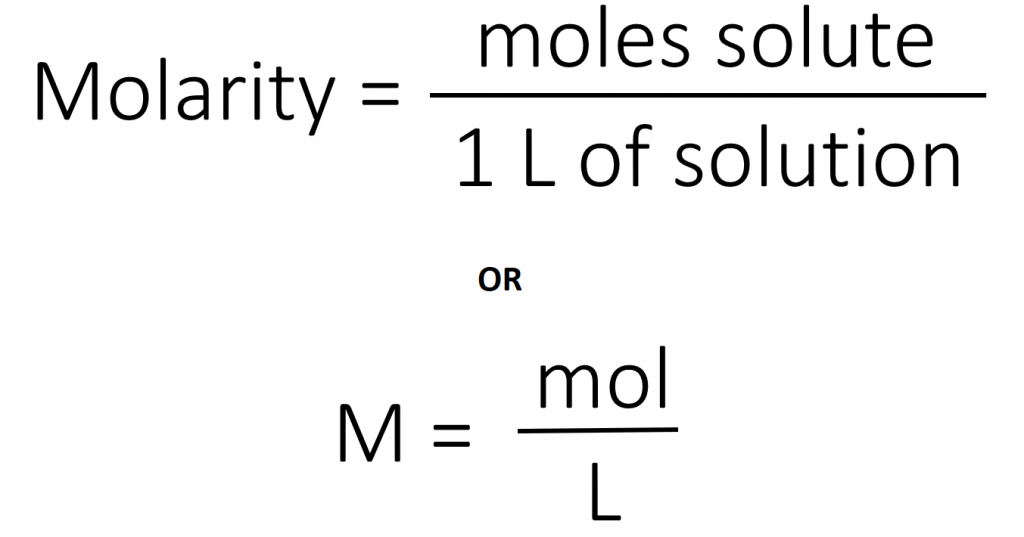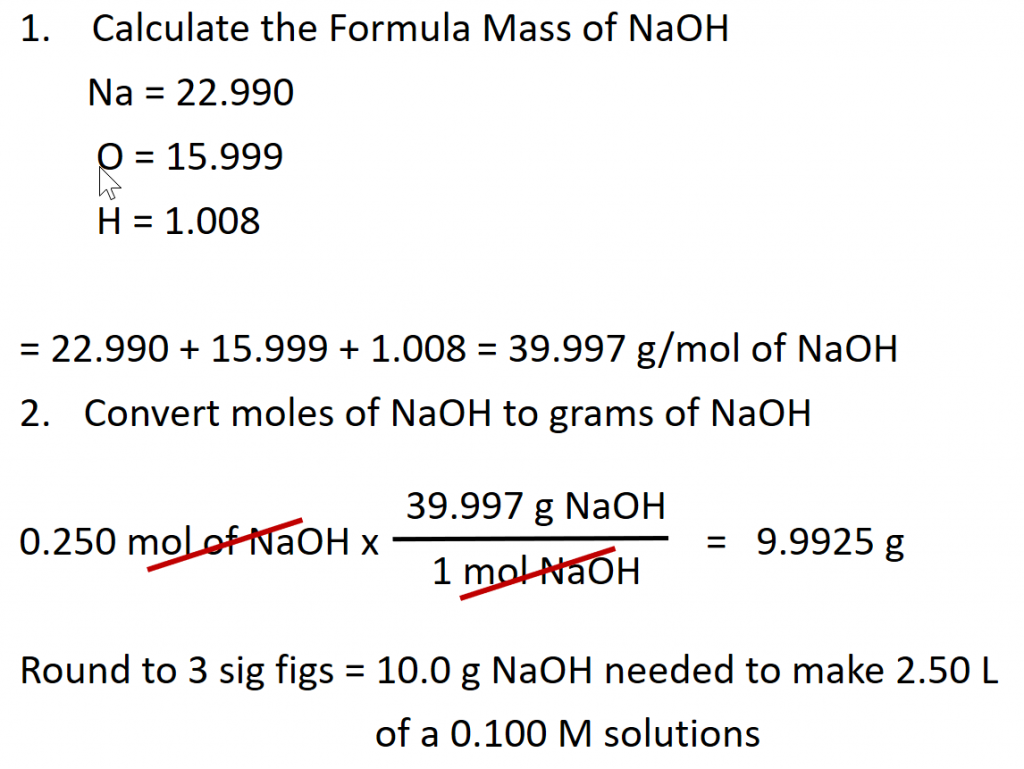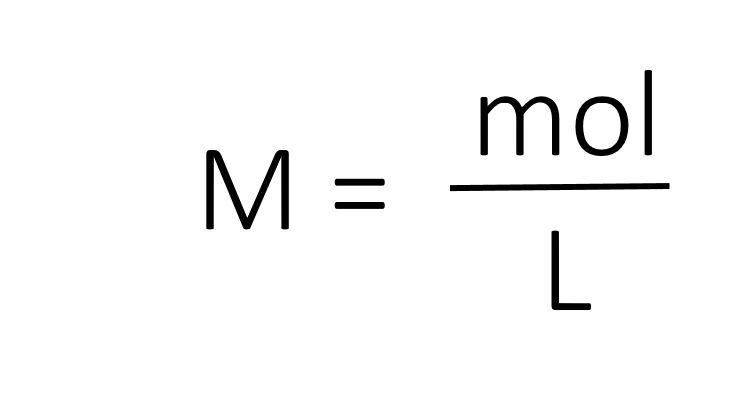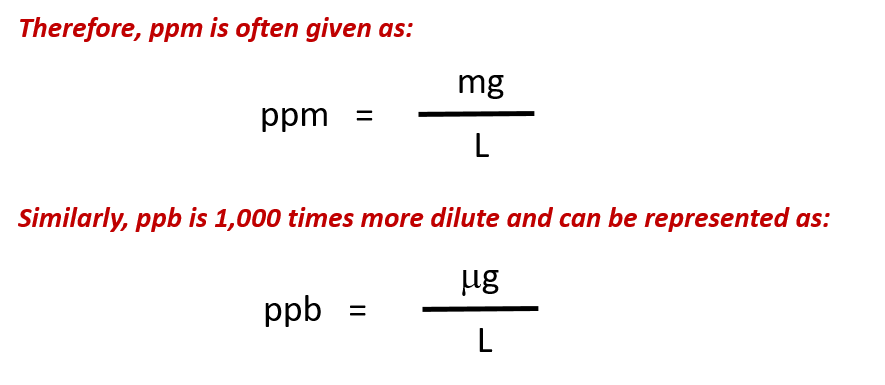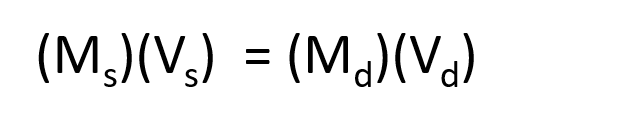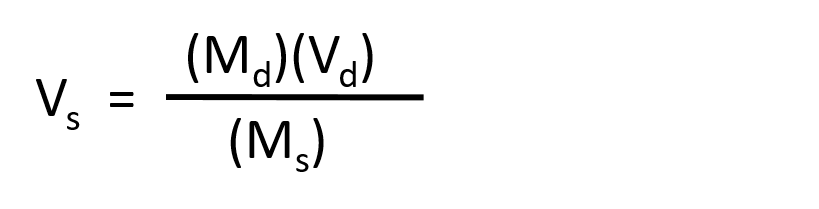Home » Student Resources » Online Chemistry Textbooks » CH103: Allied Health Chemistry » CH103 – Chapter 8: Homeostasis and Cellular Function
MenuCH103: Allied Health Chemistry
Chapter 8: Homeostasis and Cellular Function
This text is published under creative commons licensing. For referencing this work, please click here.
8.1 The Concept of Homeostasis
8.2 Disease as a Homeostatic Imbalance
8.3 Measuring Homeostasis to Evaluate Health
8.4 Solubility
8.5 Solution Concentration
8.5.1 Molarity
8.5.2 Parts Per Solutions
8.5.3 Equivalents
8.6 Dilutions
8.7 Ion Concentrations in Solution
8.8 Movement of Molecules Across the Membrane
8.9 Summary
8.10 References
8.1 The Concept of Homeostasis
Homeostasis refers to the body’s ability to physiologically regulate its inner environment to ensure its stability in response to fluctuations in external or internal conditions. The liver, the pancreas, the kidneys, and the brain (hypothalamus, the autonomic nervous system and the endocrine system) help maintain homeostasis. The liver is responsible for metabolizing toxic substances and with signaling from the pancreas maintains carbohydrate metabolism. The liver also helps to regulate lipid metabolism and is the primary site of cholesterol production. The kidneys are responsible for regulating blood water levels, re-absorption of substances into the blood, maintenance of salt and ion levels in the blood, regulation of blood pH, and excretion of urea and other waste products. The hypothalamus is involved in the regulation of body temperature, heart rate, blood pressure, and circadian rhythms (which include wake/sleep cycles).
Homeostasis can be influenced by either internal or existing conditions (instrinsic factors) or external or environmental conditions (extrinsic factors) and is maintained by many different mechanisms. All homeostatic control mechanisms have at least three interdependent components for the variable being regulated:
- A sensor or receptor that detects changes in the internal or external environment. An example is peripheral chemoreceptors, which detect changes in blood pH.
- The integrating center or control center receives information from the sensors and initiates the response to maintain homeostasis. The most important example is the hypothalamus, a region of the brain that controls everything from body temperature to heart rate, blood pressure, satiety (fullness), and circadian rhythms (including, sleep and wake cycles).
- An effector is any organ or tissue that receives information from the integrating center and acts to bring about the changes needed to maintain homeostasis. One example is the kidney, which retains water if blood pressure is too low.
The sensors, integrating center, and effectors are the basic components of every homeostatic response. Positive and negative feedback are more complicated mechanisms that enable these three basic components to maintain homeostasis for more complex physiological processes.
Negative Feedback
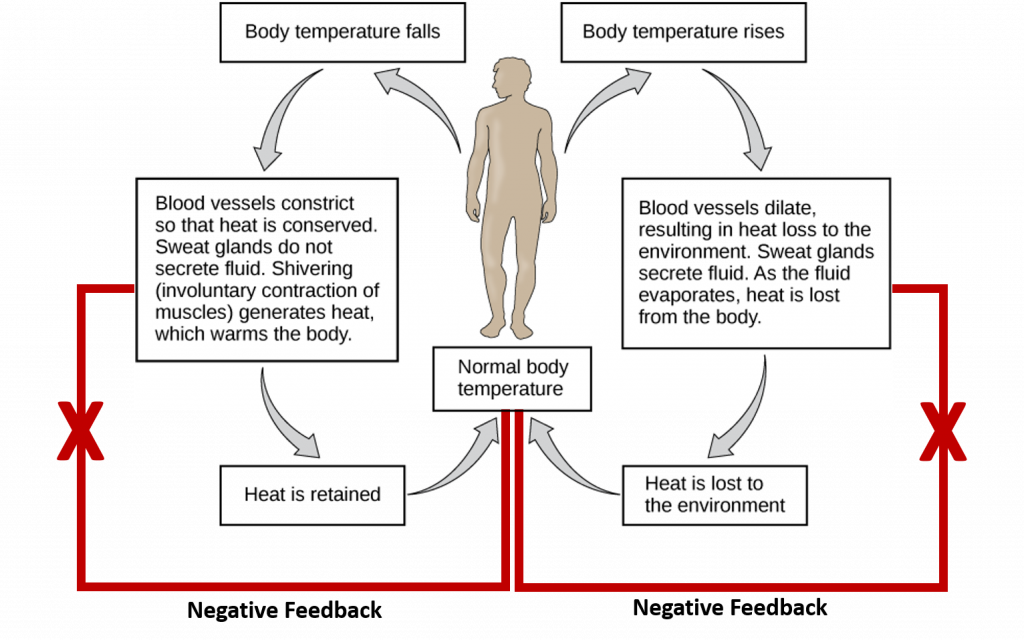
Negative feedback mechanisms use one of the products of the reaction to reduce the output or activity of the process for the purpose of returning an organ or system to its normal range of functioning. Most homeostatic processes use negative feedback regulation to maintain a specific parameter around a setpoint range that supports life Figure 8.1. However, it should be noted that negative feedback processes are also used for other processes that are not homeostatic.
Within the realm of homeostasis, temperature control is a good example that uses negative feedback. Nerve cells (the sensors) relay information about body temperature to the hypothalamus (the integrating center). The hypothalamus then signals several effectors to return the body temperature to 37oC (the set point). Two effectors activated in the process when core temperature is too high are the sweat glands which serve to cool the skin and the blood vessels which undergo vasodilation (or enlarging) so the body can give off more heat. Once the core temperature is brought back into normal range, the sensor will send negative feedback messages to the integrating center to turn off the process (ie turn off the sweat glands and inhibit further vasodilation). Both internal and external events can induce negative feedback mechanisms. The two examples above represent internal mechanisms utilized to return the body within the normal temperature range. However, we can also mediate the cooling of the body through external factors, such as removing a warm hat and gloves or pouring a cool glass of water over our head. Both external and internal mechanisms for cooling can return the temperature of the body to within the normal range and elicit the negative feedback response. Similarly, if body temperature is below the set point, muscles shiver to generate heat and the constriction of the blood vessels helps the body retain heat.
Homeostatic processes are very complex because the setpoint or normal range might change depending on the circumstance. For example, the hypothalamus can change the body’s temperature set point, such as raising it during a fever to help fight an infection.
Figure 8.1 Homeostatic Regulation of Temperature in Humans. Core body temperature is maintained at a normal setpoint of 37oC. If the core temperature rises above (right hand side) or drops below (left hand side) the setpoint, internal biological responses are initiated to return the core temperature back to the setpoint range. Once this is achieved, negative feedback loops are initiated to down regulate the internal biological responses so that the core temperature doesn’t overshoot the required change.
This Figure is adapted from: The Kahn Academy
Positive Feedback
Positive feedback is a mechanism in which an activated component enhances or further upregulates the process that gave rise to itself in order to create an even stronger response. Positive feedback mechanisms are designed to accelerate or enhance the output created by a stimulus that has already been activated. Positive feedback mechanisms are designed to push levels out of normal ranges and are not used as often in homeostatic responses. To achieve positive feedback, a series of events initiates a cascading process that builds to increase the effect of the stimulus.
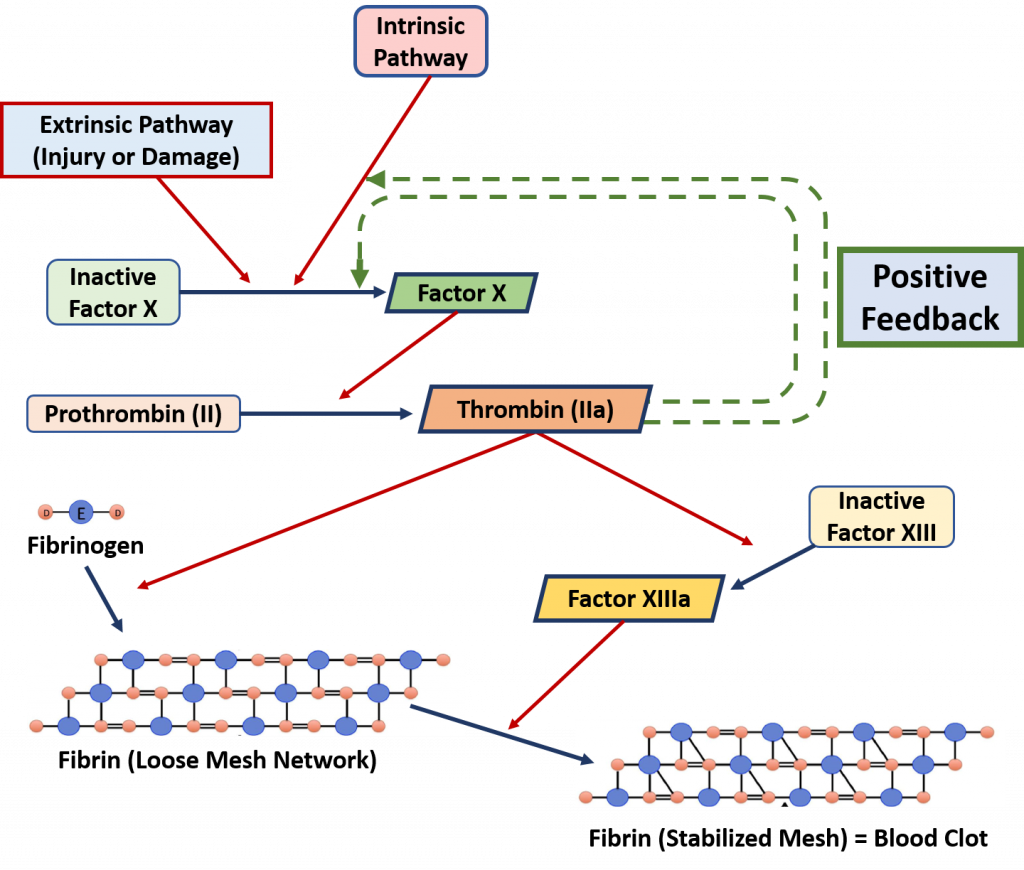
An example of a positive feedback loop is the blood clotting cascade which is originally initiated by external damage to the vasculature (Figure 8.2). During a damage event, extrinsic factors begin the initiation of the blood clotting cascade. The proteins involved in this process are usually held inactive by being produced in a much larger form than is required. To activate the protein, the protein needs to be cleaved into a smaller, active complex. When a protein is held in a large inactive state and cleaved to yield the active component, it is called a zymogen. The blood clotting cascade contains many zymogens. The first zymogen to be activated is Factor X. When Factor X is cleaved, it becomes active and proceeds to cleave the next downstream target, Prothrombin II. This produces the active component, Thrombin IIa which has multiple effects. First, it cleaves the protein Fibrinogen to produce Fibrin. Fibrin then begins to form a clotting complex with itself. This is referred to as the loose mesh network. Activated Thrombin IIa also cleaves the inactive form of Factor XIII. Activated Factor XIIIa causes crosslinks to form in the loose mesh network creating the finalized stable mesh that forms the blood clot. To accelerate this process further, Thrombin IIa also has two positive feedback effects. It can also cleave Inactive Factor X creating more activated Factor X and ultimately more activated Throbmin IIa. It also increases the activity of the instrinsic blood clotting cascade, which further upregulates the activation of Factor X.
Figure 8.2 The Positive Feedback Mechanism of the Blood Clotting Cascade. Extrinsic factors such as damage or injury activated the cleavage of zymogen proteins in the blood clotting cascade. Activation of the zymogen, Thrombin IIa begins the formation of the fibrin clotting network and also elicits positive feedback that further upregulates the entire clotting cascade.
This Figure is adapted from: MPT-Matthew
Many parameters are regulated within the body within a narrow homeostatic window to maintain proper functioning and balance within biological systems. Some examples of homeostatic parameters include:
Temperature
Humans are warm-blooded or endothermic, maintaining a near-constant body temperature. Thermoregulation is an important aspect of human homeostasis. Heat is mainly produced by the liver and muscle contractions. Humans have been able to adapt to a great diversity of climates, including hot humid and hot arid environments. High temperatures pose serious stresses for the human body, placing it in great danger of injury or even death. In order to deal with these climatic conditions, humans have developed physiologic and cultural modes of adaptation. When internal temperature reaches extremes of 45°C (113°F), hyperthermia, a condition where an individual’s body temperature is elevated beyond normal, occurs and cellular proteins will denature, causing metabolism to stop and ultimately lead to death. Hypothermia is the opposite condition, where internal body temperature falls below homeostatic norms. Hypothermia occurs when body core temperatures fall below 35.0 °C (95.0 °F). Symptoms depend on the temperature. In mild hypothermia there is shivering and mental confusion. In moderate hypothermia shivering stops and confusion increases. In severe hypothermia, there may be paradoxical undressing, in which a person removes their clothing, as well as an increased risk of the heart stopping. Hypothermia has two main types of causes. It classically occurs from exposure to extreme cold. It may also occur from any condition that decreases heat production or increases heat loss. Commonly this includes alcohol intoxication but may also include low blood sugar, anorexia, and advanced age.
Iron
Iron is an essential element for human beings. The control of this necessary but potentially toxic substance is an important part of many aspects of human health and disease. Hematologists have been especially interested in the system of iron metabolism because iron is essential to red blood cells. In fact, most of the human body’s iron is contained in red blood cells’ hemoglobin protein where it aids in the binding and transport of oxygen for cellular respiration, and iron deficiency is the most common cause of anemia.
When body levels of iron are too low, an iron-sensitive hormone called hepcidin is decreased in the duodenal epithelium (lining of the small intestine). This causes an increase in ferroportin activity, an iron-selective protein channel embedded in the membrane of intestinal cells. Activation of this channel stimulates iron uptake in the digestive system. An iron surplus will stimulate the reverse of this process.
Sugar
Blood glucose is regluated with two hormones, insulin and glucagon, both released from the pancreas.
When blood sugar levels become too high, insulin is released from the pancreas. Glucose, or sugar, is taken up by cells (especially liver and muscle tissue) where it is stored as glycogen. This results in a lowering of the blood sugar levels. On the other hand, when blood sugar levels become too low, glucagon is released by the pancreas. It promotes the breakdown of glycogen into the glucose monomers within liver cells. The liver cells then release free glucose back into the blood stream and restore blood sugar levels.
Improper glucagon functioning results in hypoglycemia, a condition where blood sugar is too low. This can be life threatening leading to coma and death if not treated promptly. Improper insulin function results in hyperglycemia or increased blood sugar levels. If this state is prolonged the disease called diabetes results. Diabetes will be discussed in more detail in section 8.2 below.
Osmoregulation
Osmoregulation is the active regulation of the osmotic pressure of bodily fluids to maintain the homeostasis of the body’s water content; that is it keeps the body’s fluids from becoming too dilute or too concentrated. Osmotic pressure is a measure of the tendency of water to move into one solution from another by osmosis. The higher the osmotic pressure of a solution the more water wants to go into the solution.
The kidneys are used to remove excess ions (such as Na+, K+ and Ca2+) from the blood, thus affecting the osmotic pressure. These are then expelled as urine. The kidneys are also important for maintaining acid/base levels, such that the pH of the blood remains close to the neutral point.
Water Volume
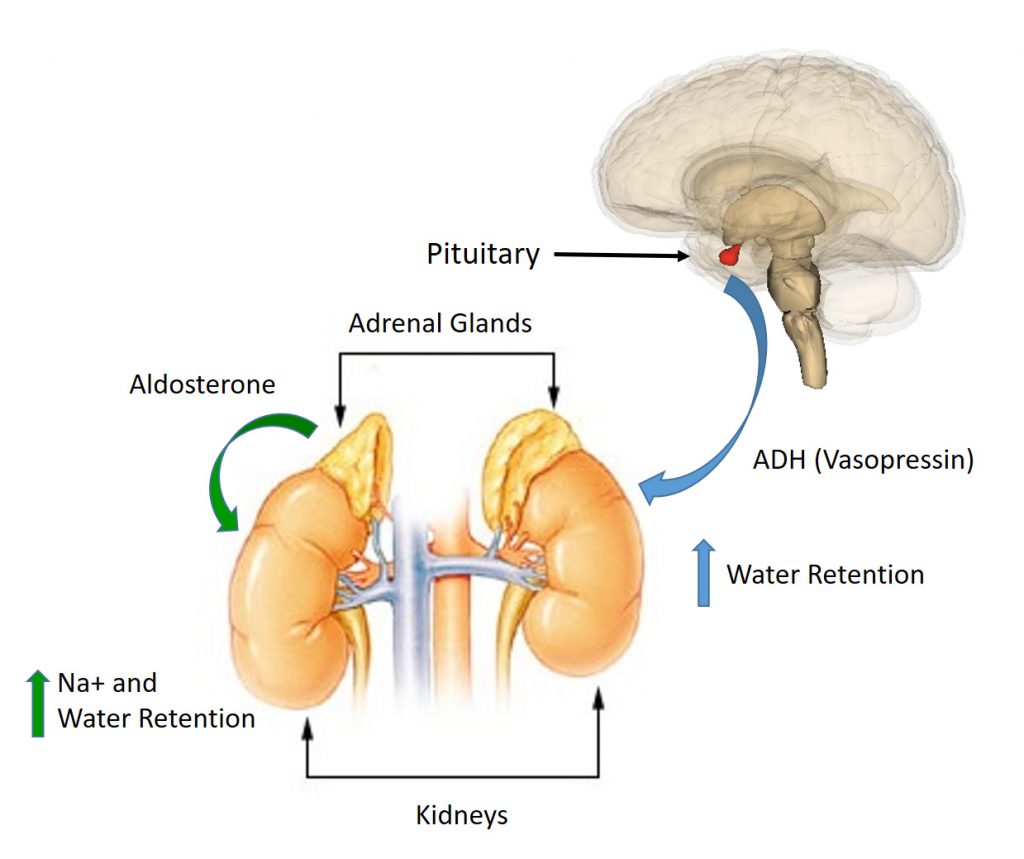
The kidneys also determine the overall water volume maintained within the body. The hormones Anti-Diuretic Hormone (ADH), also known as vasopressin, and Aldosterone play a major role in regulating kidney function.
- If the body is becoming fluid-deficient, there will be an increase in the secretion of ADH from the pituitary gland. This hormone then travels to the distal tubules or collecting ducts of the kidneys, causing fluid to be retained and urine output to be reduced. Similarly, the hormone aldosterone, a mineralcorticoid hormone with a steroid backbone, is secreted from the adrenal cortex. Aldosterone causes the kidneys to reabsorb Na+. As Na+ is reabsored, water is reabsorbed as well. Thus, Na+ retention also leads to fluid retention (Figure 8.3).
- Conversely, if fluid levels are excessive, secretion of the hormone (aldosterone) is suppressed, resulting in less retention of fluid by the kidneys and a subsequent increase in the volume of urine produced.
Figure 8.3: Effects of Aldosterone and ADH on Kidney Function. When fluid levels in the body are low, ADH (Vasopressin) is secreted by the pituitary gland and Aldosterone is secreted by the adrenal glands. ADH decreases the loss of water whereas Aldosterone increases the reabsorbtion of Na+ within the collecting duct of the kidneys. Water is reabsorbed with the Na+ causing an increase in fluid retention and decreased urine output.
This figure has been modified from: EEOC and Wikimedia Commons.
Hemostasis
Hemostasis is the process whereby bleeding is halted. A major part of this is the coagulation cascade highlighted in Figure 8.2.
Platelet accumulation causes blood clotting in response to a break or tear in the lining of blood vessels. Unlike the majority of control mechanisms in human body, the hemostasis utilizes positive feedback, for the more the clot grows, the more clotting occurs, until the blood stops.
Sleep
Sleep timing depends upon a balance between homeostatic sleep propensity, the need for sleep as a function of the amount of time elapsed since the last adequate sleep episode, and circadian rhythms which determine the ideal timing of a correctly structured and restorative sleep episode. A sleep deficit will elicit a compensatory increase in the intensity and duration of sleep, while excessive sleep reduces sleep propensity.
8.2 Disease as a Homeostatic Imbalance
What Is Disease?
Disease is any failure of normal physiological function that leads to negative symptoms. While disease is often a result of infection or injury, most diseases involve the disruption of normal homeostasis. Anything that prevents positive or negative feedback system from working correctly could lead to disease if the mechanisms of disruption become strong enough.
Aging is a general example of disease as a result of homeostatic imbalance. As an organism ages, weakening of feedback loops gradually results in an unstable internal environment. This lack of homeostasis increases the risk for illness and is responsible for the physical changes associated with aging. Heart failure is the result of negative feedback mechanisms that become overwhelmed, allowing destructive positive feedback mechanisms to compensate for the failed feedback mechanisms. This leads to high blood pressure and enlargement of the heart, which eventually becomes too stiff to pump blood effectively, resulting in heart failure. Severe heart failure can be fatal.
Diabetes: A Disease of Failed Homeostasis
Diabetes, a metabolic disorder caused by excess blood glucose levels, is a key example of disease caused by failed homeostasis. In ideal circumstances, homeostatic control mechanisms should prevent this imbalance from occurring. However, in some people, the mechanisms do not work efficiently enough or the amount of blood glucose is too great to be effectively managed. In these cases, medical intervention is necessary to restore homeostasis and prevent permanent organ damage.
Normal Blood Sugar Regulation
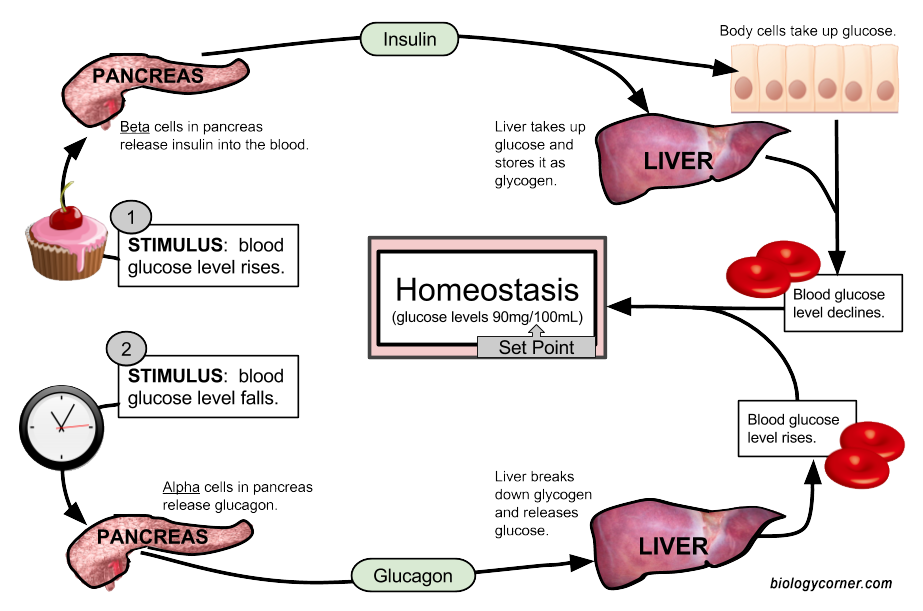
The human body maintains constant levels of glucose throughout the day. After a meal, blood glucose levels rise, as glucose is transported from the small intestine into the blood stream. In response to this, the pancreas (the sensor) releases insulin into the bloodstream where it acts as a hormone. As you learned in Chapter 6, hormones are molecules that are made in one part of the body, secreted into the bloodstream and are transported to a distant part of the body, where they mediate an effect or reaction at that secondary target. Insulin is a peptide hormone that is released by the pancreas in response to elevated levels of blood glucose. Insulin binds with high efficiency to receptor proteins on the surface of liver cells, where it turns on signaling within the liver to increase the uptake of glucose from the bloodstream (Figure 8.4). Other body cells, such as skeletal muscle, adipose tissue, and brain cells are also activated by insulin. When a molecule has multiple different effects on the body, these multiple effects are called pleiotropic effects. These other cell types will also take up glucose to use as an energy source. This lowers blood glucose levels back to normal levels. The liver can take up more glucose than other tissue types and convert it into a large carbohydrate molecule called glycogen, that you learned about in Chapter 6. It is stored as this carbohydrate until glucose is needed when it can then be broken down to released back into the blood stream. Up to 10% of the volume in liver cells is in the form of glycogen.
Figure 8.4 Glucose Homeostasis. When blood sugar rises due to a meal (Path 1), the pancreas senses the increase in blood glucose levels. In response, it releases the peptide hormone, insulin. Insulin interacts with downstream target cells in the body, including liver and muscle tissue, where it causes the uptake of glucose from the blood stream into the cell. The excess glucose is stored as the carbohydrate, glycogen. This returns blood glucose levels back to normal. If it has been several hours after eating a mean, blood glucose levels will begin to fall (Path 2). This signals liver cells to breakdown glycogen into glucose monomers. The glucose can then be realeased back into the bloodstream.
Figure is by: Shannan Muskopf from Biologycorner.com
In between meals or during times of fasting, blood glucose levels begin to drop. This activates the pancreas to secrete a different hormone, called glucagon. Glucagon signaling activates the liver to begin breaking down the glycogen storage molecule into free glucose. The glucose is then released back into the blood stream, increasing blood glucose levels (Figure 8.4).
Over the course of a day, blood glucose levels will fluctuate modestly around the homeostatic set point (Figure 8.5). As meals are eaten, this triggers a rise in blood glucose that is counteracted by the secretion of insulin. In between meals, blood glucose levels fall, and glucagon is released by the pancreas to signal to the liver to release glucose back into the blood stream.
Figure 8.5. Homeostasis of Glucose Metabolism: This image illustrates glucose metabolism over the course of a day. Homeostasis may become imbalanced if the pancreas is overly stressed, making it unable to balance glucose metabolism. This can lead to diabetes.
Causes of Homeostatic Disruption
People with type 1 diabetes do not produce insulin due to auto-immune destruction of the insulin producing cells, while people with type 2 diabetes have chronic high blood glucose levels that cause insulin resistance to develop. With diabetes, blood glucose is increased by normal glucagon activity, but the lack of or resistance to insulin means that blood sugar levels are unable to return to normal. This causes metabolic changes that result in diabetes symptoms like weakened blood vessels and frequent urination. Diabetes is normally treated with insulin injections, which replaces the missing negative feedback of normal insulin secretions. If diabetes is left untreated or becomes resistant to treatment, more serious side effects are seen, including peripheral neuropathy (loss of feeling in the extremities), loss of circulation in the extremities, blurred vision and/or blindness.
Overall, Diabetes is a disease caused by a broken feedback loop involving the hormone insulin. The broken feedback loop makes it difficult or impossible for the body to bring high blood sugar down to a healthy level.
8.3. Measuring Homeostasis to Evaluate Health
Since homeostatic imbalances can lead to disease states or even death, homeostasis has been identified as one of the eight core concepts of biology. The American Association of Medical Colleges reports that a physicians ability to identify and apply knowledge about homeostasis should be regarded as one of their key competencies. Thus, physicians need a way to evaluate the homeostatic health of their patients. They need to be able to evaluate the mixtures of compounds that are found within the human body.
Recall that in Chapter 2, you were introduced to the concept of a mixture, which is a substance that is composed of two or more substances. Also recall that mixtures can be of two types: Homogeneous and Heterogeneous, where homogeneous mixtures combine so intimately that they are observed as a single substance, even though they are not. Heterogeneous mixtures, on the other hand, are non-uniform and have regions of the mixture that look different from other regions of the mixture. Homogeneous mixtures can be further broken down into two classifications: Colloids and Solutions. A colloid is a mixture that contains particles with diameters ranging from 2 to 500 nm. Colloids appear uniform in nature and have the same composition throughout but are cloudy or opaque. Blood is a good example of a colloid. True solutions, on the other hand, have particle sizes of a typical ion or small molecule (~0.1 to 2 nm in diameter) and are transparent, although they may be colored. The remaining sections of this chapter will focus on the characteristics of true solutions.
Solutions are all around us. Air, for example, is a solution. If you live near a lake, a river, or an ocean, that body of water is not pure H2O but most probably a solution. Much of what we drink—for example, soda, coffee, tea, and milk are solutions. Solutions are a large part of everyday life. A lot of the chemistry occurring around us happens in solution. In fact, much of the chemistry that occurs in our own bodies takes place in solution, and many solutions—such as the Ringer’s lactate IV solution—are important in healthcare. In our understanding of chemistry, we need to understand a little bit about solutions. In this chapter, you will learn about the special characteristics of solutions, how solutions are characterized, and some of their properties.
(Back to the Top)
Types of Solutions
Material exists in three states: solid, liquid, and gas. Solutions also exist in all these states:
- Gaseous mixtures are usually homogeneous and are commonly gas-gas solutions. For quantitative treatment of this type of solutions, we will devote a unit to gases. The atmosphere is a gaseous solution that consists of nitrogen, oxygen, argon, carbon dioxide, water, methane, and some other minor components. Some of these components, such as water, oxygen, and carbon dioxide may vary in concentration in different locations on the Earth depending on factors such as temperature and altitude.
- When molecules of gas, solid or liquid are dispersed and mixed with those of liquid, the homogeneous (uniform) states are called liquid solutions. Solids, liquids and gases dissolve in a liquid solvent to form liquid solutions. In this chapter, most of the chemistry that we will discuss occurs in liquid solutions where water is the solvent.
- Many alloys, ceramics, and polymer blends are solid solutions. Within a certain range, copper and zinc dissolve in each other and harden to give solid solutions called brass. Silver, gold, and copper form many different alloys with unique colors and appearances. Alloys and other solid solutions are important in the world of materials chemistry.
(Back to the Top)
8.4 Solubility
The maximum amount of a substance that can be dissolved in a given volume of solvent is called solubility. Often, the solubility in water is expressed in gram/100 mL. A solution that has not reached its maximum solubility is called an unsaturated solution. This means that more solute could still be added to the solvent and dissolving would still occur.
A solution that has reached the maximum solubility is called a saturated solution. If more solute is added at this point, it will not dissolve into the solution. Instead it will remain precipitated as a solid at the bottom of the solution. Thus, one can often tell that a solution is saturated if extra solute is present (this can exist as another phase, such as gas, liquid, or solid). In a saturated solution there is no net change in the amount of solute dissolved, but the system is by no means static. In fact, the solute is constantly being dissolved and deposited at an equal rate. Such a phenomenon is called equilibrium. For example:
In special circumstances, a solution may be supersaturated. Supersaturated solutions are solutions that have dissolved solute beyond the normal saturation point. Usually a condition such as increased temperature or pressure is required to create a supersaturated solution. For example, sodium acetate has a very high solubility at 270 K. When cooled, such a solution stays dissolved in what is called a meta-stable state. However, when a seeding crystal is added to the solution, the extra solute will rapidly solidify. During the crystallization process, heat is evolved, and the solution becomes warm. Common hand warmers use this chemical process to generate heat.
Video showing the crystallization of a supersaturated solution of sodium acetate. Video by : North Carolina School of Science and Mathematics
So how can we predict the solubility of a substance?
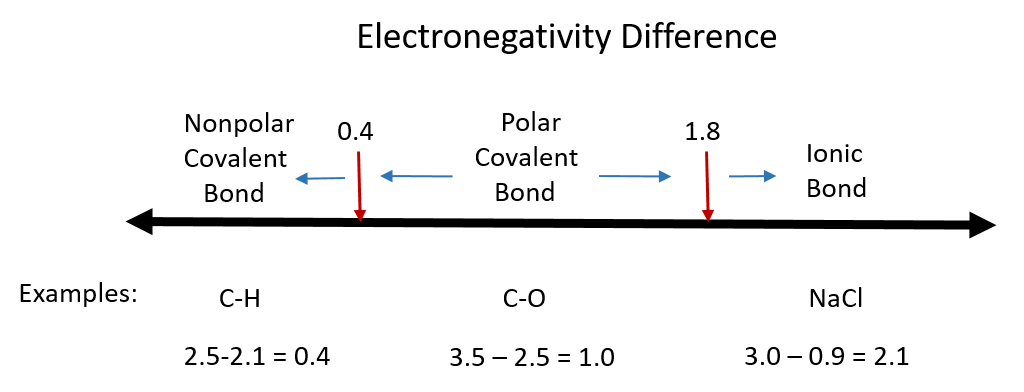
One useful classification of materials is polarity. As you read about covalent and ionic compounds in Chapters 3 and 4, you learned that ionic compounds have the highest polarity forming full cations and anions within each molecule as electrons are donated from one atom to another. You also learned that covalent bonds could be polar or nonpolar in nature depending on whether or not the atoms involved in the bond share the electrons unequally or equally, respectively. Recall that the electronegativity difference can be used to determine the polarity of a substance. Typically an ionic bond has an electronegativity difference of 1.8 or above, whereas a polar covalent bond is between 0.4 to 1.8, and a nonpolar covalent bond is 0.4 or below.
Figure 8.6 Electronegativity Difference Diagram. The diagram above is a guide for discerning what type of bond forms between two different atoms. By taking the difference between the electronegativity values for each of the atoms involved in the bond, the bond type and polarity can be predicted. Note that full ionic character is rarely reached, however when metals and nonmetals form bonds, they are named using the rules for ionic bonding.
Substances with zero or low electronegativity difference such as H2, O2, N2, CH4, CCl4 are nonpolar compounds, whereas H2O, NH3, CH3OH, NO, CO, HCl, H2S, PH3 higher electronegativity difference are polar compounds. Typically compounds that have similar polarity are soluble in one another. This can be described by the rule:
Like Dissolves Like.
This means that substances must have similar intermolecular forces to form solutions. When a soluble solute is introduced into a solvent, the particles of solute can interact with the particles of solvent. In the case of a solid or liquid solute, the interactions between the solute particles and the solvent particles are so strong that the individual solute particles separate from each other and, surrounded by solvent molecules, enter the solution. (Gaseous solutes already have their constituent particles separated, but the concept of being surrounded by solvent particles still applies.) This process is called solvation and is illustrated in Figure 7.2. When the solvent is water, the word hydration, rather than solvation, is used.
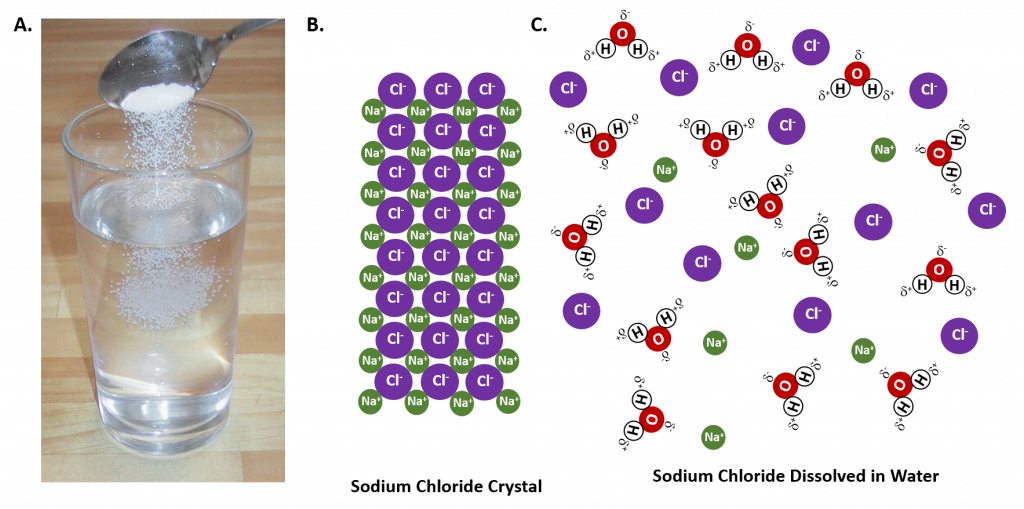
In general polar solvents dissolve polar solutes whereas nonpolar solvents will dissolve nonpolar solutes. Overall, the solution process depends on the strength of the attraction between the solute particles and the solvent particles. For example, water is a highly polar solvent that is capable of dissolving many ionic salts. Figure 8.7 shows the solution process, where water act as the solvent to dissolve the crystalline salt, sodium chloride (NaCl). Note that when ionic compounds dissolve in a solvent they break apart into free floating ions in solution. This enables the compound to interact with the solvent. In the case of water dissolving sodium chloride, the sodium ion is attracted to the partial negative charge of the oxygen atom in the water molecule, whereas the chloride ion is attracted to the partial positive hydrogen atoms.
Figure 8.7: The Process of Dissolving. When an ionic salt, such as sodium chloride, shown in (A), comes into contact with water, the water molecules dissociate the ion molecules of the sodium chloride into their ionic state, shown as a molecular model in (B) the solid crystalline lattice of sodium chloride, and (C) the sodium chloride dissolved in the water solvent. (Photo of sodium chloride provided by Chris 73 ).
Many ionic compounds are soluble in water, however, not all ionic compounds are soluble. Ionic compounds that are soluble in water exist in their ionic state within the solution. You will notice in Figure 7.2 that the sodium chloride breaks apart into the sodium ion and the chloride ion as it dissolves and interacts with the water molecules. For ionic compounds that are not soluble in water, the ions are so strongly attracted to one another that they cannot be broken apart by the partial charges of the water molecules.
The dissociation of soluble ionic compounds gives solutions of these compounds an interesting property: they conduct electricity. Because of this property, soluble ionic compounds are referred to as electrolytes. Many ionic compounds dissociate completely and are therefore called strong electrolytes. Sodium chloride is an example of a strong electrolyte. Some compounds dissolve but dissociate only partially, and solutions of such solutes may conduct electricity only weakly. These solutes are called weak electrolytes. Acetic acid (CH3COOH), the compound in vinegar, is a weak electrolyte. Solutes that dissolve into individual neutral molecules without dissociation do not impart additional electrical conductivity to their solutions and are called nonelectrolytes. Polar covalent compounds, such as table sugar (C12H22O11), are good examples of nonelectrolytes.
The term electrolyte is used in medicine to mean any of the important ions that are dissolved in aqueous solution in the body. Important physiological electrolytes include Na+, K+, Ca2+, Mg2+, and Cl−. Sports drinks such as Gatoraid have combinations of these key electrolytes, to help replenish electrolyte loss following a hard workout.
Similarly, solutions can also be made by mixing two compatible liquids together. The liquid in the lower concentration is termed the solute, and the one in higher concentration the solvent. For example, grain alcohol (CH3CH2OH) is a polar covalent molecule that can mix with water. When two similar solutions are placed together and are able to mix into a solution, they are said to be miscible. Liquids that do not share similar characteristics and cannot mix together, on the other hand, are termed immiscible. For example, the oils found in olive oil, such as oleic acid (C18H34O2) have mainly nonpolar covalent bonds which do not have intermolecular forces that are strong enough to break the hydrogen bonding between the water molecules. Thus, water and oil do not mix and are said to be immiscible.
Other factor such as temperature and pressure also affects the solubility of a solvent. Thus, in specifying solubility, one should also be aware of these other factors.
8.5 Solution Concentration
In chemistry, concentration is defined as the abundance of a constituent divided by the total volume of a mixture. All of us have a qualitative idea of what is meant by concentration. Anyone who has made instant coffee or lemonade knows that too much powder gives a strongly flavored, highly concentrated drink, whereas too little results in a dilute solution that may be hard to distinguish from water. Quantitatively, the concentration of a solution describes the quantity of a solute that is contained in a particular quantity of that solution. Knowing the concentration of solutes is important in controlling the stoichiometry of reactants for reactions that occur in solution, and are critical for many aspects of our lives, from measuring the correct dose of medicine to detecting chemical pollutants like lead and arsenic. Chemists use many different ways to define concentrations. In this section, we will cover the most common ways of presenting solution concentration. These include: Molarity and Parts Per Solutions.
8.5.1 Molarity
The most common unit of concentration is molarity, which is also the most useful for calculations involving the stoichiometry of reactions in solution. The molarity (M) of a solution is the number of moles of solute present in exactly 1 L of solution.
The units of molarity are therefore moles per liter of solution (mol/L), abbreviated as M. Note that the volume indicated is the total volume of the solution and includes both the solute and the solvent. For example, an aqueous solution that contains 1 mol (342 g) of sucrose in enough water to give a final volume of 1.00 L has a sucrose concentration of 1.00 mol/L or 1.00 M. In chemical notation, square brackets around the name or formula of the solute represent the concentration of a solute. So
[sucrose] = 1.00 M
is read as “the concentration of sucrose is 1.00 molar.” The equation above can be used to calculate how much solute is required to make any amount of a desired solution.
Example Problem:
Calculate the number of moles of sodium hydroxide (NaOH) needed to make 2.50 L of 0.100 M NaOH.
Given: (1) identity of solute = NaOH, (2) volume = 2.50 L, and (3) molarity of solution = 0.100 mol/L (Note: when calculating problems always write out the units of molarity as mol/L, rather than M. This will allow you to cancel out your units when doing the calculation.)
Asked for: amount of solute in moles
Strategy: (1) Rearrange the equation above to solve for the desired unit, in this case for moles. (2) Double check all the units in the equation and make sure they match. Perform any conversions that are needed so that the units match. (3) Fill in values appropriately and do the math.
Solution:
(1) Rearrange the equation above to solve for moles.
(2) Double check all the units in the equation and make sure they match.
The given values for this equation are the volume 2.50 L and the molarity 0.100 mol/L. The volume units for both of these numbers are in Liters (L) and thus, match. Therefore, no conversions need to be made.
(3) Fill in values appropriately and do the math.
Preparation of Solutions
Note that in the example above, we still don’t have enough information to actually make the solution in the laboratory. There is no piece of equipment that can measure out the moles of a substance. For this, we need to convert the number of moles of the sample into the number of grams represented by that number. We can then easily use a balance to weigh the amount of substance needed for the solution. For the example above:
To actually make the solution, it is typical to dissolve the solute in a small amount of the solvent and then once the solute is dissolved, the final volume can be brought up to 2.50 L. If you were to add 10 g of NaOH directly to 2.50 L, the final volume would be larger than 2.50 L and the solution concentration would be less than 0.100 M. Remember that the final volume must include both the solute and the solvent.
Figure 8.8 illustrates the procedure for making a solution of cobalt(II) chloride dihydrate in ethanol. Note that the volume of the solvent is not specified. Since the solute occupies space in the solution, the volume of the solvent needed is less than the desired total volume of solution.

Figure 8.8: Preparation of a Solution of Known Concentration Using a Solid Solute. To make a solution, start by addition a portion of the solvent to the flask. Next, weigh out the appropriate amount of solute and slowly add it to the solvent. Once it is dissolved in the solvent, the volume of the solution can be brought up to the final solution volume. For the volumetric flask shown, this is indicated by the black line in the neck of the flask. In this case, it indicates 500 mL of solution. Volumetric flasks exist in many different sizes to accommodate different solution volumes. Graduated cylinders can also be used to accurately bring a solution to its final volume. Other glassware, including beakers and Erlenmeyer flasks are not accurate enough to make most solutions.
Example Molarity Calculation
The solution in Figure 7.8 contains 10.0 g of cobalt(II) chloride dihydrate, CoCl2·2H2O, in enough ethanol to make exactly 500 mL of solution. What is the molar concentration of CoCl2·2H2O?
Given: mass of solute and volume of solution
Asked for: concentration (M)
Strategy:
1. We know that Molarity equals moles/Liter
2. To calculate Molarity, we need to express:
- the mass in the form of moles
- the volume in the form of Liters
- Plug both into the equation above and calculate
Solution:
- Converting the mass into moles. We can use the molar mass to convert the grams of CoCl2·2H2O to moles.
- The molar mass of CoCl2·2H2O is 165.87 g/mol (and includes the two water molecules as they are part of the crystal lattice structure of this solid hydrate!)
2. Convert the volume into Liters
3. Plug values into the Molarity equation:
8.5.2 Parts Per Solutions
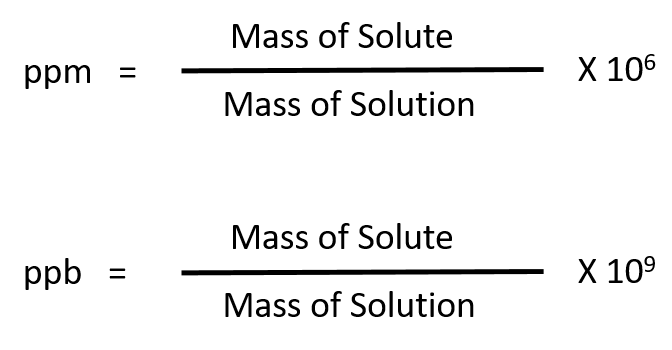
In the consumer and industrial world, the most common method of expressing the concentration is based on the quantity of solute in a fixed quantity of solution. The “quantities” referred to here can be expressed in mass, in volume, or both (i.e., the mass of solute in a given volume of solution.) In order to distinguish among these possibilities, the abbreviations (m/m), (v/v) and (m/v) are used.
In most applied fields of Chemistry, (m/m) measure is often used, whereas in clinical chemistry, (m/v) is commonly used, with mass expressed in grams and volume in mL.
One of the more common ways to express such concentrations as “parts per 100“, which we all know as “percent“. “Cent” is the Latin-derived prefix relating to the number 100
(L. centum), as in century or centennial. It also denotes 1/100th (from L. centesimus) as in centimeter and the monetary unit cent. Percent solutions define the quantity of a solute that is dissolved in a quantity of solution multiplied by 100. Percent solutions can be expressed in terms of mass solute per mass solution (m/m%), or mass solute per volume of solution (m/v%), or volume of solute per volume of solution (v/v%). When making a percent solution, it is important to indicate what units are being used, so that others can also make the solution properly. Also, recall that the solution is the sum of both the solvent and the solute when you are performing percent calculations.
Solution = Solute + Solvent
Thus, the following equation can be used when calculating percent solutions:
Example 1:
As an example, a 7.0% v/v solution of ethanol in water, would contain 7 mL of ethanol in a total of 100 mL of solution. How much water is in the solution?
In this problem, we know that the:
Solution = Solute + Solvent
Thus, we can fill in the values and then solve for the unknown.
100 mL = 7 mL + X mL of Solvent (in this case water)
shifting the 7 over to the other side, we can see that:
100 mL – 7 mL = 93 mL H2O
Example 2
What is the (m/v)% of a solution if 24.0 g of sucrose is dissolved in a total solution of 243 mL?
Example 3
How many grams of NaCl are required to make 625 mL of a 13.5% solution?
For more dilute solutions, parts per million (106 ppm) and parts per billion (109; ppb) are used. These terms are widely employed to express the amounts of trace pollutants in the environment.
Like percentage (“part per hundred”) units, ppm and ppb may be defined in terms of masses, volumes, or mixed mass-volume units. There are also ppm and ppb units defined with respect to numbers of atoms and molecules.
The mass-based definitions of ppm and ppb are given here:
Both ppm and ppb are convenient units for reporting the concentrations of pollutants and other trace contaminants in water. Concentrations of these contaminants are typically very low in treated and natural waters, and their levels cannot exceed relatively low concentration thresholds without causing adverse effects on health and wildlife. For example, the EPA has identified the maximum safe level of fluoride ion in tap water to be 4 ppm. Inline water filters are designed to reduce the concentration of fluoride and several other trace-level contaminants in tap water (Figure 8.9).
Figure 8.9. (a) In some areas, trace-level concentrations of contaminants can render unfiltered tap water unsafe for drinking and cooking. (b) Inline water filters reduce the concentration of solutes in tap water. (credit a: modification of work by Jenn Durfey; credit b: modification of work by “vastateparkstaff”/Wikimedia commons
When reporting contaminants like lead in drinking water, ppm and ppb concentrations are often reported in mixed unit values of mass/volume. This can be very useful as it is easier for us to think about water in terms of its volume, rather than by its mass. In addition, the density of water is 1.0 g/mL or 1.0 mg/0.001 mL which makes the conversion between the two units easier. For example, if we find that there is lead contamination in water of 4 ppm, this would mean that there are:
8.5.3 Equivalents
Concentrations of ionic solutes are occasionally expressed in units called equivalents (Eq). One equivalent equals 1 mol of positive or negative charge. Thus, 1 mol/L of Na+(aq) is also 1 Eq/L because sodium has a 1+ charge. A 1 mol/L solution of Ca2+(aq) ions has a concentration of 2 Eq/L because calcium has a 2+ charge. Dilute solutions may be expressed in milliequivalents (mEq)—for example, human blood plasma has a total concentration of about 150 mEq/L.
In a more formal definition, the equivalent is the amount of a substance needed to do one of the following:
- react with or supply one mole of hydrogen ions (H+) in an acid–base reaction
- react with or supply one mole of electrons in a redox reaction.
By this definition, an equivalent is the number of moles of an ion in a solution, multiplied by the valence of that ion. If 1 mol of NaCl and 1 mol of CaCl2 dissolve in a solution, there is 1 equiv Na, 2 equiv Ca, and 3 equiv Cl in that solution. (The valence of calcium is 2, so for that ion you have 1 mole and 2 equivalents.)
(Back to the Top)
8.6 Dilutions
A solution of a desired concentration can also be prepared by diluting a small volume of a more concentrated solution with additional solvent. A stock solution, which is a prepared solution of known concentration, is often used for this purpose. Diluting a stock solution is preferred when making solutions of very weak concentrations, because the alternative method, weighing out tiny amounts of solute, can be difficult to carry out with a high degree of accuracy. Dilution is also used to prepare solutions from substances that are sold as concentrated aqueous solutions, such as strong acids.
The procedure for preparing a solution of known concentration from a stock solution is shown in Figure 8.10. It requires calculating the amount of solute desired in the final volume of the more dilute solution and then calculating the volume of the stock solution that contains this amount of solute. Remember that diluting a given quantity of stock solution with solvent does not change the amount of solute present, only the volume of the solution is changing. The relationship between the volume and concentration of the stock solution and the volume and concentration of the desired diluted solution can therefore be expressed mathematically as:
Where Ms is the concentration of the stock solution, Vs is the volume of the stock solution, Md is the concentration of the diluted solution, and Vd is the volume of the diluted solution.
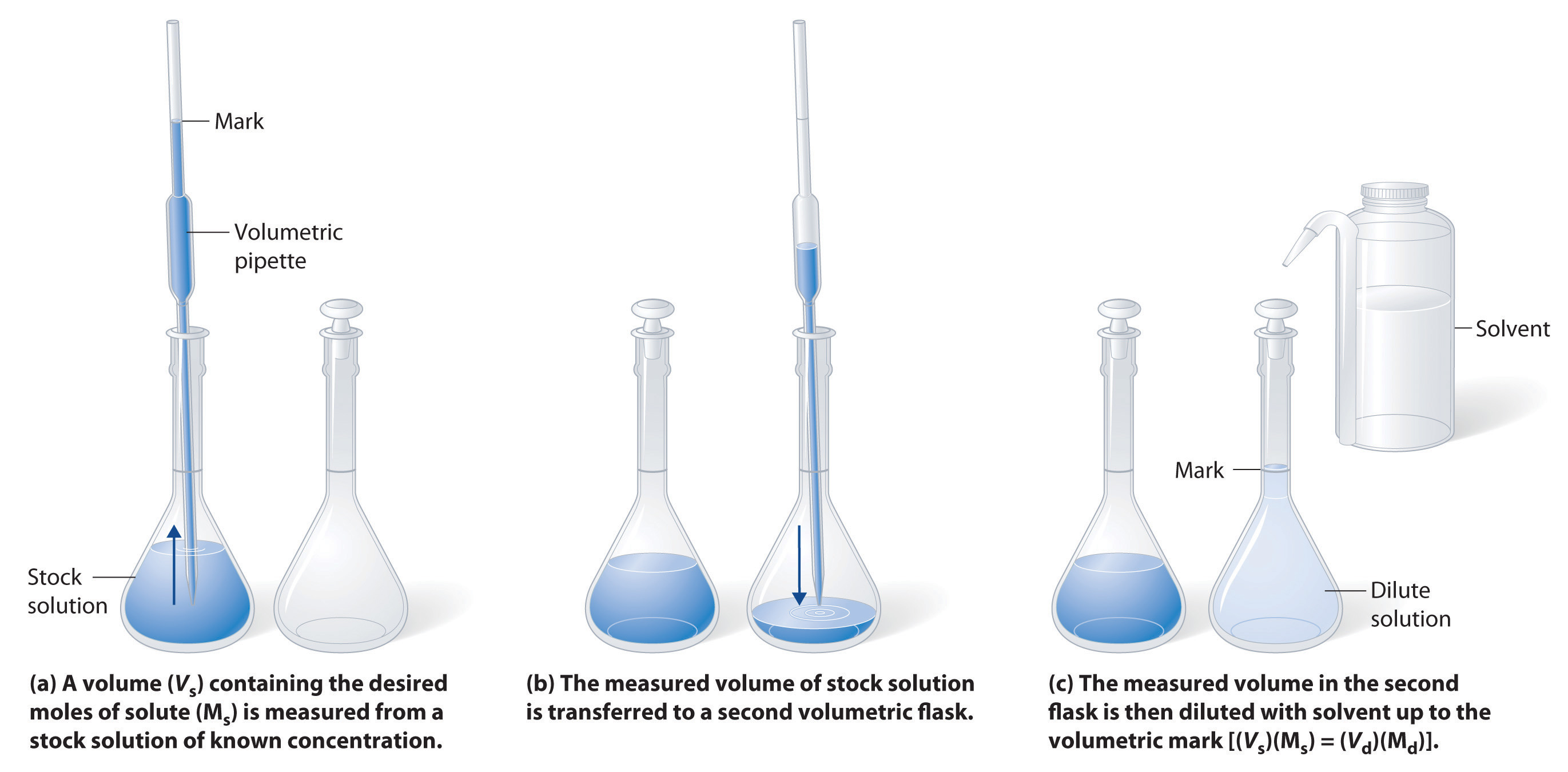
Figure 8.10 Preparation of a Solution of Known Concentration by Diluting a Stock Solution. (a) A volume (Vs) containing the desired amount of solute (Ms) is measured from a stock solution of known concentration. (b) The measured volume of stock solution is transferred to a second volumetric flask. (c) The measured volume in the second flask is then diluted with solvent up to the volumetric mark [(Vs)(Ms) = (Vd)(Md)].
Example of Dilution Calculations
What volume of a 3.00 M glucose stock solution is necessary to prepare 2500 mL of 0.400 M solution?
Given: volume and molarity of dilute solution, and molarity of stock solution
Asked for: volume of stock solution
Strategy and Solution:
For Dilution problems, as long as you know 3 of the variables, you can solve for the 4th variable.
- Start by rearranging the equation to solve for the variable that you want to find. In this case, you want to find the volume of the stock solution, Vs
2. Next, check to make sure that like terms have the same units. For example, Md and Ms are both concentrations, thus, to be able to perform the calculations, they should be in the same unit (in this case they are both listed in Molarity). If the concentrations were different, say one was given in Molarity and the other in percent or one was in Molarity and the other was in Millimolarity, one of the terms would need to be converted so that they match. That way, the units will cancel out and leave you with units of volume, in this case.
3. Finally, fill in the equation with known values and calculate the final answer.
Note that if 333mL of stock solution is needed, that you can also calculate the amount of solvent needed to make the final dilution. (Total volume – volume of stock solution = volume of solvent needed for the final dilution. In this case 2,500 mL – 333 mL = 2,167 mL of water needed to make the final dilution (this should be done in a graduated cylinder or volumetric flask).
(Back to the Top)
8.7 Ion Concentrations in Solution
Thus far, we have been discussing the concentration of the overall solution in terms of total solute divided by the volume of the solution. Let’s consider in more detail exactly what that means when considering ionic and covalent compounds. When ionic compounds dissolve in a solution, they break apart into their ionic state. Cations and anions associate with the polar water molecules. Recall that solutions that contain ions are called electrolyotes, due to their ability to conduct electricity. For example, ammonium dichromate (NH4)2Cr2O7 is an ionic compound that contains two NH4+ ions and one Cr2O72− ion per formula unit. Like other ionic compounds, it is a strong electrolyte that dissociates in aqueous solution to give hydrated NH4+ and Cr2O72− ions. If we consider this this solution mathematically, we can see that for every ammonium dichromate molecule that dissolves, there will be three resulting ions that form (the two NH4+ ions and the one Cr2O72− ion). This can also be thought of on a larger molar scale. When 1 mole of (NH4)2Cr2O7 is dissolved, it results in 3 moles of ions (1 mol of Cr2O72− anions and 2 mol of NH4+ cations) within the solution (Figure 8.11). To discuss the relationship between the concentration of a solution and the resulting number of ions, the term equivalents is used.
One equivalent is defined as the amount of an ionic compound that provides 1 mole of electrical charge (+ or -). It is calculated by dividing the molarity of the solution by the total charge created in the solution.
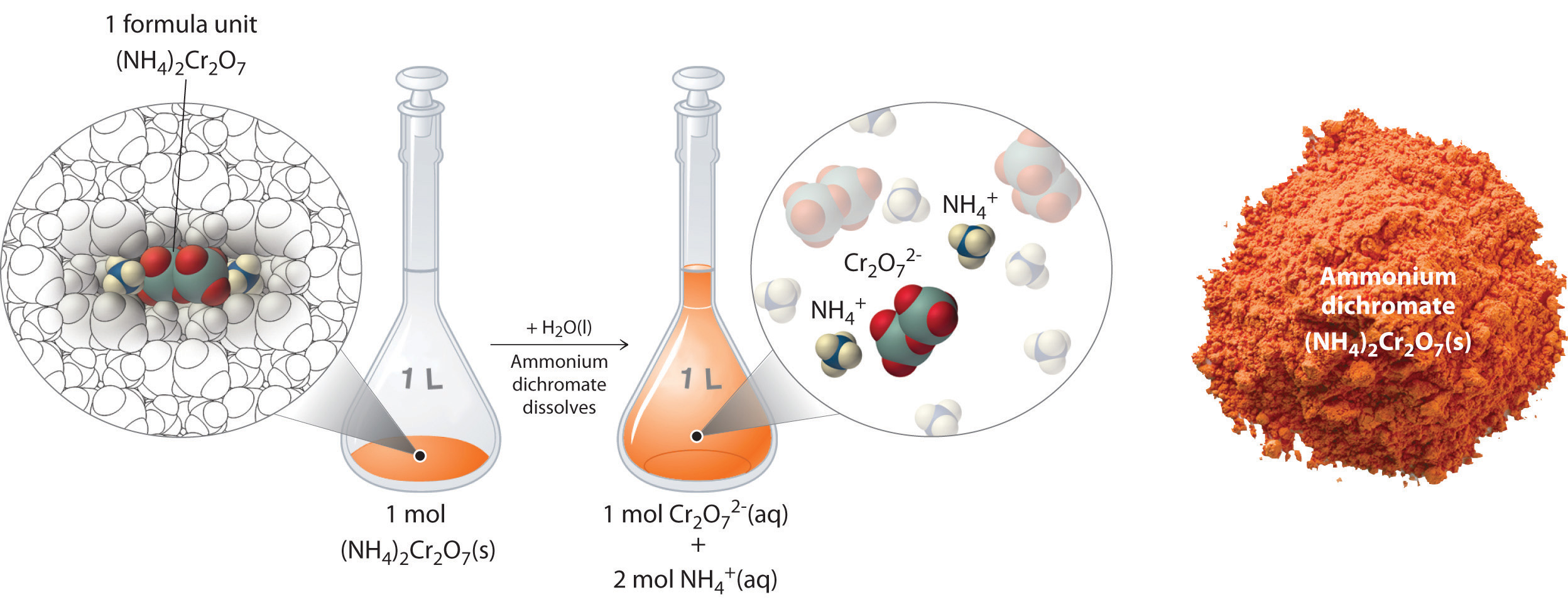
Figure 8.11 Dissolution of 1 mol of an Ioncic Compound. Dissoliving 1 mol of ammonium dichromate formula units in water produces 1 mol of Cr2O72− anions and 2 mol of NH4+ cations. (Water molecules are omitted from a molecular view of the solution for clarity.)
When we carry out a chemical reaction using a solution of a salt such as ammonium dichromate, we need to know the concentration of each ion present in the solution. If a solution contains 1.43 M (NH4)2Cr2O7, then the concentration of Cr2O72− must also be 1.43 M because there is one Cr2O72− ion per formula unit. However, there are two NH4+ ions per formula unit, so the concentration of NH4+ ions is 2 × 1.43 M = 2.86 M. Because each formula unit of (NH4)2Cr2O7 produces three ions when dissolved in water (2NH4+ + 1Cr2O72−), the total concentration of ions in the solution is 3 × 1.43 M = 4.29 M. The equivalent value of (NH4)2Cr2O7 can then be calculated by dividing 1.43 M by 4.29 M, yielding 0.333 equivalents. Thus, for (NH4)2Cr2O7, dissolving 0.333 moles of the compound will yield 1 mole of ions in the solution.
Example 1
What are the concentrations of all ionic species derived from the solutes in these aqueous solutions?
- 0.21 M NaOH
- 3.7 M (CH3)CHOH
- 0.032 M In(NO3)3
Given: molarity
Asked for: concentrations
Strategy:
A Classify each compound as either a strong electrolyte or a nonelectrolyte.
B If the compound is a nonelectrolyte, its concentration is the same as the molarity of the solution. If the compound is a strong electrolyte, determine the number of each ion contained in one formula unit. Find the concentration of each species by multiplying the number of each ion by the molarity of the solution.
Solution:
1. 0.21 M NaOH
A Sodium hydroxide is an ionic compound that is a strong electrolyte (and a strong base) in aqueous solution:
B Because each formula unit of NaOH produces one Na+ ion and one OH− ion, the concentration of each ion is the same as the concentration of NaOH: [Na+] = 0.21 M and [OH−] = 0.21
2. 3.7 M (CH3)CHOH
A The formula (CH3)2CHOH represents 2-propanol (isopropyl alcohol) and contains the –OH group, so it is an alcohol. Recall from Section 4.1 “Aqueous Solutions” that alcohols are covalent compounthat dissolve in water to give solutions of neutral molecules. Thus alcohols are nonelectrolytes
B The only solute species in solution is therefore (CH3)2CHOH molecules, so [(CH3)2CHOH] = 3.7 M
3. 0.032 M In(NO3)3
A Indium nitrate is an ionic compound that contains In3+ ions and NO3− ions, so we expect it to behave like a strong electrolyte in aqueous solution
B One formula unit of In(NO3)3 produces one In3+ ion and three NO3− ions, so a 0.032 M In(NO3)3 solution contains 0.032 M In3+ and 3 × 0.032 M = 0.096 M NO3–—that is, [In3+] = 0.032 M and [NO3−] = 0.096 M
(Back to the Top)
8.8 Movement of Molecules Across the Membrane
One of the great wonders of the cell membrane is its ability to regulate the concentration of substances inside the cell. These substances include ions such as Ca++, Na+, K+, and Cl–; nutrients including sugars, fatty acids, and amino acids; and waste products, particularly carbon dioxide (CO2), which must leave the cell.
The membrane’s lipid bilayer structure provides the first level of control. The phospholipids are tightly packed together, and the membrane has a hydrophobic interior. This structure causes the membrane to be selectively permeable. A membrane that has selective permeability allows only substances meeting certain criteria to pass through it unaided. In the case of the cell membrane, only relatively small, nonpolar materials can move through the lipid bilayer (remember, the lipid tails of the membrane are nonpolar). Some examples of these are other lipids, oxygen and carbon dioxide gases, and alcohol. However, water-soluble materials—like glucose, amino acids, and electrolytes—need some assistance to cross the membrane because they are repelled by the hydrophobic tails of the phospholipid bilayer. All substances that move through the membrane do so by one of two general methods, which are categorized based on whether or not energy is required. Passive transport is the movement of substances across the membrane without the expenditure of cellular energy. In contrast, active transport is the movement of substances across the membrane using energy from adenosine triphosphate (ATP). You have seen examples of these types of transport mechanisms in Chapter 4, where we learned about the generation of an action potential within a neuron.
Passive Transport
In order to understand how substances move passively across a cell membrane, it is necessary to understand concentration gradients and diffusion. A concentration gradient is the difference in concentration of a substance across a space. Molecules (or ions) will spread/diffuse from where they are more concentrated to where they are less concentrated until they are equally distributed in that space. (When molecules move in this way, they are said to move down their concentration gradient.) Diffusion is the movement of particles from an area of higher concentration to an area of lower concentration. A couple of common examples will help to illustrate this concept. Imagine being inside a closed bathroom. If a bottle of perfume were sprayed, the scent molecules would naturally diffuse from the spot where they left the bottle to all corners of the bathroom, and this diffusion would go on until no more concentration gradient remains. Another example is a spoonful of sugar placed in a cup of tea. Eventually the sugar will diffuse throughout the tea until no concentration gradient remains. In both cases, if the room is warmer or the tea hotter, diffusion occurs even faster as the molecules are bumping into each other and spreading out faster than at cooler temperatures. Having an internal body temperature around 98.6° F thus also aids in diffusion of particles within the body.
Whenever a substance exists in greater concentration on one side of a semipermeable membrane, such as the cell membranes, any substance that can move down its concentration gradient across the membrane will do so. Consider substances that can easily diffuse through the lipid bilayer of the cell membrane, such as the gases oxygen (O2) and CO2. O2 generally diffuses into cells because it is more concentrated outside of them, and CO2 typically diffuses out of cells because it is more concentrated inside of them. Neither of these examples requires any energy on the part of the cell, and therefore they use passive transport to move across the membrane.
Before moving on, you need to review the gases that can diffuse across a cell membrane. Because cells rapidly use up oxygen during metabolism, there is typically a lower concentration of O2 inside the cell than outside. As a result, oxygen will diffuse from the interstitial fluid directly through the lipid bilayer of the membrane and into the cytoplasm within the cell. On the other hand, because cells produce CO2 as a byproduct of metabolism, CO2 concentrations rise within the cytoplasm; therefore, CO2 will move from the cell through the lipid bilayer and into the interstitial fluid, where its concentration is lower. This mechanism of molecules moving across a cell membrane from the side where they are more concentrated to the side where they are less concentrated is a form of passive transport called simple diffusion (Figure 8.12).
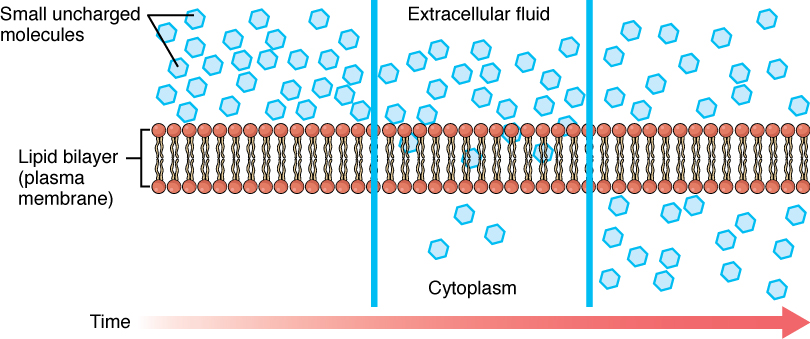
Figure 8.12. Simple Diffusion across the Cell (Plasma) Membrane. The structure of the lipid bilayer allows small, uncharged substances such as oxygen and carbon dioxide, and hydrophobic molecules such as lipids, to pass through the cell membrane, down their concentration gradient, by simple diffusion.
Large polar or ionic molecules, which are hydrophilic, cannot easily cross the phospholipid bilayer. Very small polar molecules, such as water, can cross via simple diffusion due to their small size. Charged atoms or molecules of any size cannot cross the cell membrane via simple diffusion as the charges are repelled by the hydrophobic tails in the interior of the phospholipid bilayer. Solutes dissolved in water on either side of the cell membrane will tend to diffuse down their concentration gradients, but because most substances cannot pass freely through the lipid bilayer of the cell membrane, their movement is restricted to protein channels and specialized transport mechanisms in the membrane. Facilitated diffusion is the diffusion process used for those substances that cannot cross the lipid bilayer due to their size, charge, and/or polarity (Figure 8.13). A common example of facilitated diffusion is the movement of glucose into the cell, where it is used to make ATP. Although glucose can be more concentrated outside of a cell, it cannot cross the lipid bilayer via simple diffusion because it is both large and polar. To resolve this, a specialized carrier protein called the glucose transporter will transfer glucose molecules into the cell to facilitate its inward diffusion.
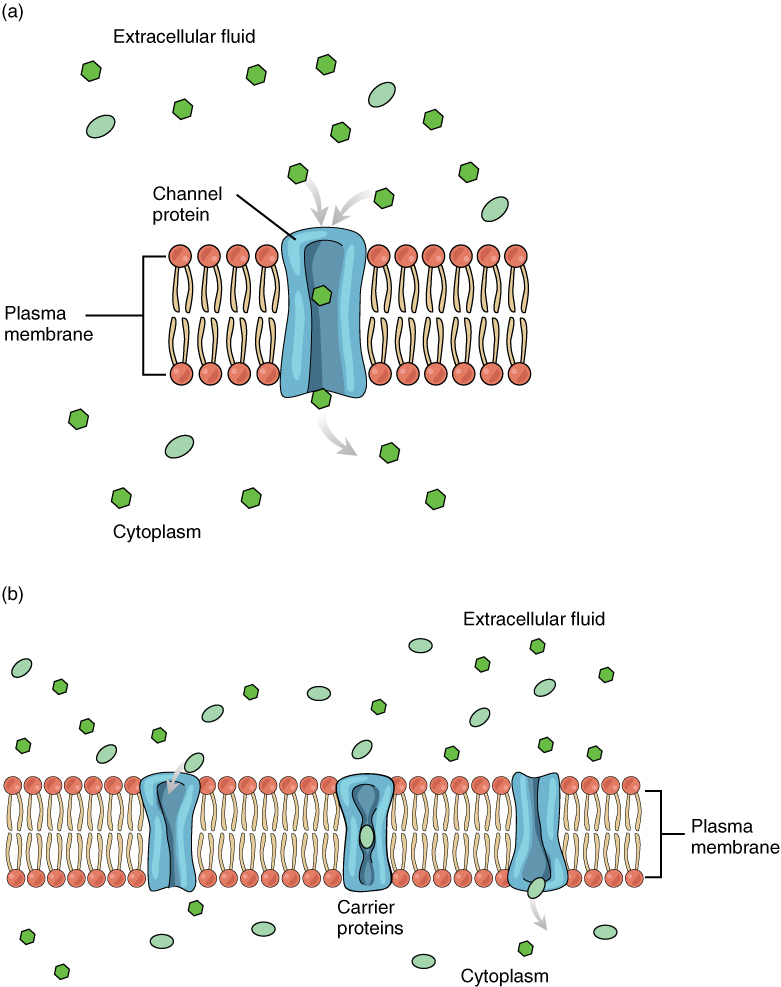
As an example, even though sodium ions (Na+) are highly concentrated outside of cells, these electrolytes are charged and cannot pass through the nonpolar lipid bilayer of the membrane. Their diffusion is facilitated by membrane proteins that form sodium channels (or “pores”), so that Na+ ions can move down their concentration gradient from outside the cells to inside the cells. There are many other solutes that must undergo facilitated diffusion to move into a cell, such as amino acids, or to move out of a cell, such as wastes. Because facilitated diffusion is a passive process, it does not require energy expenditure by the cell.
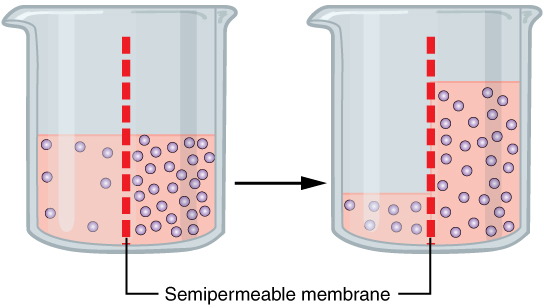
Water also can move freely across the cell membrane of all cells, either through protein channels or by slipping between the lipid tails of the membrane itself. Osmosis is the diffusion of water through a semipermeable membrane (Figure 8.14).
The movement of water molecules is not itself regulated by cells, so it is important that cells are exposed to an environment in which the concentration of solutes outside of the cells (in the extracellular fluid) is equal to the concentration of solutes inside the cells (in the cytoplasm). Tonicity is used to describe the variations of solute in a solution with the solute inside the cell. Three terms—hypotonic, isotonic, and hypertonic—are used to compare the relative solute concentration of a cell to that of the extracellular fluid surrounding the cells.
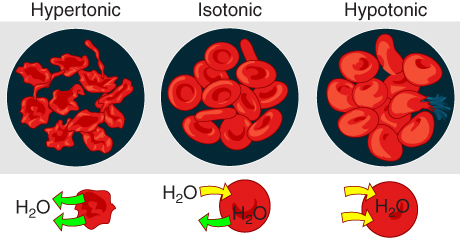
In a hypotonic solution, such as tap water, the extracellular fluid has a lower concentration of solutes than the fluid inside the cell, and water enters the cell. (Note that water is moving down its concentration gradient) If this occurs in an animal cell, the cell may burst, or lyse.
In a hypertonic solution (the prefix hyper– refers to the extracellular fluid having a higher concentration of solutes than the cell’s cytoplasm), the fluid contains less water than the cell does. Because the cell has a lower concentration of solutes, the water will leave the cell. In effect, the solute is drawing the water out of the cell. This may cause an animal cell to shrivel, or crenate.
In an isotonic solution, the extracellular fluid has the same solute concentration as the cell. If the concentration of solutes of the cell matches that of the extracellular fluid, there will be no net movement of water into or out of the cell.
Blood cells in hypertonic, isotonic, and hypotonic solutions take on characteristic appearances as shown in Figure 8.15. A critical aspect of homeostasis in living things is to create an internal environment in which all of the body’s cells are in an isotonic solution. Various organ systems, particularly the kidneys, work to maintain this homeostasis.
Some organisms, such as plants, fungi, bacteria, and some protists, have cell walls that surround the plasma membrane and prevent cell lysis. The plasma membrane can only expand to the limit of the cell wall, so the cell will not lyse. In fact, the cytoplasm in plants is always slightly hypertonic compared to the cellular environment, and water will always enter a cell if water is available. This influx of water produces turgor pressure, which stiffens the cell walls of the plant (Figure 8.16). In nonwoody plants, turgor pressure supports the plant. If the plant cells become hypertonic, as occurs in drought or if a plant is not watered adequately, water will leave the cell. Plants lose turgor pressure in this condition and wilt.
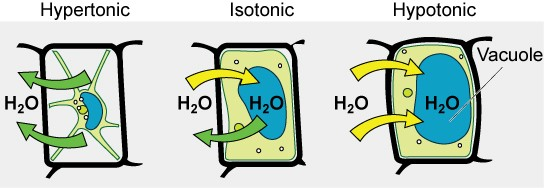
Figure 8.16 The turgor pressure within a plant cell depends on the tonicity of the surrounding solution.
Another mechanism besides diffusion to passively transport materials between compartments is filtration. Unlike diffusion of a substance from where it is more concentrated to less concentrated, filtration uses a hydrostatic pressure gradient that pushes the fluid—and the solutes within it—from a higher pressure area to a lower pressure area. Filtration is an extremely important process in the body. For example, the circulatory system uses filtration to move plasma and substances across the endothelial lining of capillaries and into surrounding tissues, supplying cells with the nutrients. Furthermore, filtration pressure in the kidneys provides the mechanism to remove wastes from the bloodstream.
Active Transport
For all of the transport methods described above, the cell expends no energy. Membrane proteins that aid in the passive transport of substances do so without the use of ATP. During active transport, ATP is required to move a substance across a membrane, often with the help of protein carriers, and usually against its concentration gradient.
One of the most common types of active transport involves proteins that serve as pumps. The word “pump” probably conjures up thoughts of using energy to pump up the tire of a bicycle or a basketball. Similarly, energy from ATP is required for these membrane proteins to transport substances—molecules or ions—across the membrane, usually against their concentration gradients (from an area of low concentration to an area of high concentration).
The sodium-potassium pump, which is also called Na+/K+ ATPase, transports sodium out of a cell while moving potassium into the cell. The Na+/K+ pump is an important ion pump found in the membranes of many types of cells. These pumps are particularly abundant in nerve cells, which are constantly pumping out sodium ions and pulling in potassium ions to maintain an electrical gradient across their cell membranes. An electrical gradient is a difference in electrical charge across a space. In the case of nerve cells, for example, the electrical gradient exists between the inside and outside of the cell, with the inside being negatively-charged (at around -70 mV) relative to the outside. The negative electrical gradient is maintained because each Na+/K+ pump moves three Na+ ions out of the cell and two K+ ions into the cell for each ATP molecule that is used (Figure 8.17). This process is so important for nerve cells that it accounts for the majority of their ATP usage.
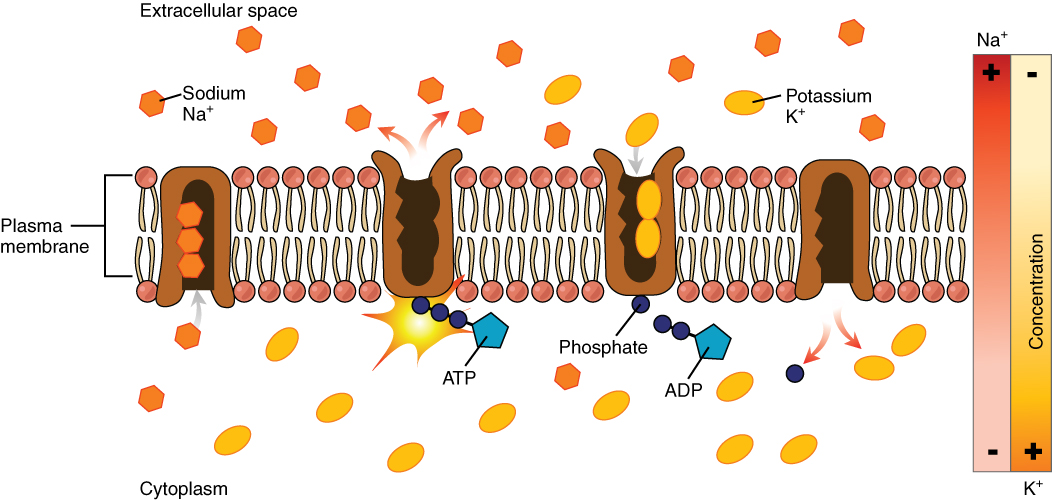
Active transport pumps can also work together with other active or passive transport systems to move substances across the membrane. For example, the sodium-potassium pump maintains a high concentration of sodium ions outside of the cell. Therefore, if the cell needs sodium ions, all it has to do is open a passive sodium channel, as the concentration gradient of the sodium ions will drive them to diffuse into the cell. In this way, the action of an active transport pump (the sodium-potassium pump) powers the passive transport of sodium ions by creating a concentration gradient. When active transport powers the transport of another substance in this way, it is called secondary active transport.
Symporters are secondary active transporters that move two substances in the same direction. For example, the sodium-glucose symporter uses sodium ions to “pull” glucose molecules into the cell. Because cells store glucose for energy, glucose is typically at a higher concentration inside of the cell than outside. However, due to the action of the sodium-potassium pump, sodium ions will easily diffuse into the cell when the symporter is opened. The flood of sodium ions through the symporter provides the energy that allows glucose to move through the symporter and into the cell, against its concentration gradient.
Conversely, antiporters are secondary active transport systems that transport substances in opposite directions. For example, the sodium-hydrogen ion antiporter uses the energy from the inward flood of sodium ions to move hydrogen ions (H+) out of the cell. The sodium-hydrogen antiporter is used to maintain the pH of the cell’s interior.
Other forms of active transport do not involve membrane carriers. Endocytosis (bringing “into the cell”) is the process of a cell ingesting material by enveloping it in a portion of its cell membrane, and then pinching off that portion of membrane (Figure 8.18). Once pinched off, the portion of membrane and its contents becomes an independent, intracellular vesicle. A vesicle is a membranous sac—a spherical and hollow organelle bounded by a lipid bilayer membrane. Endocytosis often brings materials into the cell that must to be broken down or digested. Phagocytosis (“cell eating”) is the endocytosis of large particles. Many immune cells engage in phagocytosis of invading pathogens. Like little Pac-men, their job is to patrol body tissues for unwanted matter, such as invading bacterial cells, phagocytize them, and digest them. In contrast to phagocytosis, pinocytosis (“cell drinking”) brings fluid containing dissolved substances into a cell through membrane vesicles.
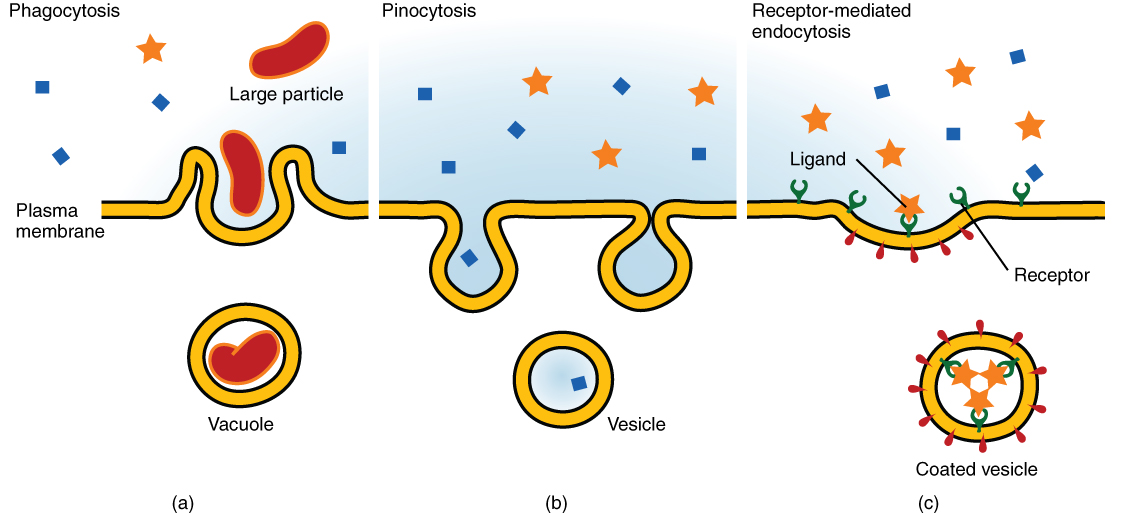
Phagocytosis and pinocytosis take in large portions of extracellular material, and they are typically not highly selective in the substances they bring in. Cells regulate the endocytosis of specific substances via receptor-mediated endocytosis. Receptor-mediated endocytosis is endocytosis by a portion of the cell membrane that contains many receptors that are specific for a certain substance. Once the surface receptors have bound sufficient amounts of the specific substance (the receptor’s ligand), the cell will endocytose the part of the cell membrane containing the receptor-ligand complexes. Iron, a required component of hemoglobin, is endocytosed by red blood cells in this way. Iron is bound to a protein called transferrin in the blood. Specific transferrin receptors on red blood cell surfaces bind the iron-transferrin molecules, and the cell endocytoses the receptor-ligand complexes.
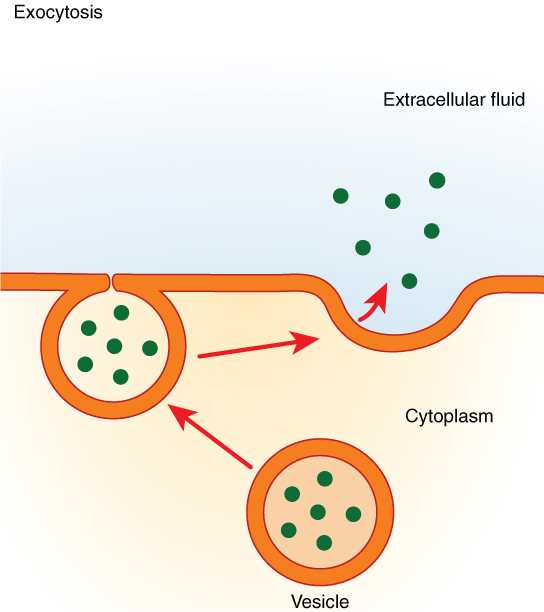
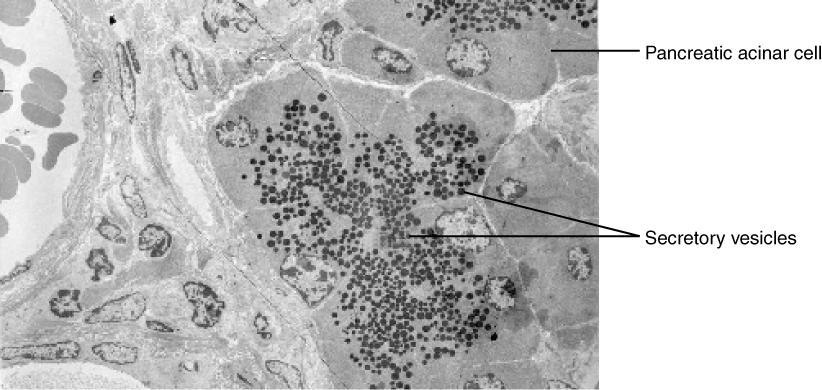
In contrast with endocytosis, exocytosis (taking “out of the cell”) is the process of a cell exporting material using vesicular transport (Figure 8.19). Many cells manufacture substances that must be secreted, like a factory manufacturing a product for export. These substances are typically packaged into membrane-bound vesicles within the cell. When the vesicle membrane fuses with the cell membrane, the vesicle releases it contents into the interstitial fluid. The vesicle membrane then becomes part of the cell membrane. Cells of the stomach and pancreas produce and secrete digestive enzymes through exocytosis (Figure 8.20). Endocrine cells produce and secrete hormones that are sent throughout the body, and certain immune cells produce and secrete large amounts of histamine, a chemical important for immune responses.
8.9 Summary
To ensure that you understand the material in this chapter, you should review the meanings of the bold terms in the following summary and ask yourself how they relate to the topics in the chapter.
A solution is a homogeneous mixture. The major component is the solvent, while the minor component is the solute. Solutions can have any phase; for example, an alloy is a solid solution. Solutes are soluble or insoluble, meaning they dissolve or do not dissolve in a particular solvent. The terms miscible and immiscible, instead of soluble and insoluble, are used for liquid solutes and solvents. The statement like dissolves like is a useful guide to predicting whether a solute will dissolve in a given solvent.
Dissolving occurs by solvation, the process in which particles of a solvent surround the individual particles of a solute, separating them to make a solution. For water solutions, the word hydration is used. If the solute is molecular, it dissolves into individual molecules. If the solute is ionic, the individual ions separate from each other, forming a solution that conducts electricity. Such solutions are called electrolytes. If the dissociation of ions is complete, the solution is a strong electrolyte. If the dissociation is only partial, the solution is a weak electrolyte. Solutions of molecules do not conduct electricity and are called nonelectrolytes.
The amount of solute in a solution is represented by the concentration of the solution. The maximum amount of solute that will dissolve in a given amount of solvent is called the solubility of the solute. Such solutions are saturated. Solutions that have less than the maximum amount are unsaturated. Most solutions are unsaturated, and there are various ways of stating their concentrations. Mass/mass percent, volume/volume percent, and mass/volume percent indicate the percentage of the overall solution that is solute. Parts per million (ppm) and parts per billion (ppb) are used to describe very small concentrations of a solute. Molarity, defined as the number of moles of solute per liter of solution, is a common concentration unit in the chemistry laboratory. Equivalents express concentrations in terms of moles of charge on ions. When a solution is diluted, we use the fact that the amount of solute remains constant to be able to determine the volume or concentration of the final diluted solution. Solutions of known concentration can be prepared either by dissolving a known mass of solute in a solvent and diluting to a desired final volume or by diluting the appropriate volume of a more concentrated solution (a stock solution) to the desired final volume.
The cell membrane provides a barrier around the cell, separating its internal components from the extracellular environment. It is composed of a phospholipid bilayer, with hydrophobic internal lipid “tails” and hydrophilic external phosphate “heads.” Various membrane proteins are scattered throughout the bilayer, both inserted within it and attached to it peripherally. The cell membrane is selectively permeable, allowing only a limited number of materials to diffuse through its lipid bilayer. All materials that cross the membrane do so using passive (non energy-requiring) or active (energy-requiring) transport processes. During passive transport, materials move by simple diffusion or by facilitated diffusion through the membrane, down their concentration gradient. Water passes through the membrane in a diffusion process called osmosis. During active transport, energy is expended to assist material movement across the membrane in a direction against their concentration gradient. Active transport may take place with the help of protein pumps or through the use of vesicles.
Practice Questions
Review Questions
1. Because they are embedded within the membrane, ion channels are examples of ________.
- receptor proteins
- integral proteins
- peripheral proteins
- glycoproteins
2. The diffusion of substances within a solution tends to move those substances ________ their ________ gradient.
- up; electrical
- up; electrochemical
- down; pressure
- down; concentration
3. Ion pumps and phagocytosis are both examples of ________.
- endocytosis
- passive transport
- active transport
- facilitated diffusion
4. Choose the answer that best completes the following analogy: Diffusion is to ________ as endocytosis is to ________.
- filtration; phagocytosis
- osmosis; pinocytosis
- solutes; fluid
- gradient; chemical energy
Critical Thinking Questions
1. What materials can easily diffuse through the lipid bilayer, and why?
2. Why is receptor-mediated endocytosis said to be more selective than phagocytosis or pinocytosis?
3. What do osmosis, diffusion, filtration, and the movement of ions away from like charge all have in common? In what way do they differ?
Key Takeaway
- Solution concentrations are typically expressed as molarity and can be prepared by dissolving a known mass of solute in a solvent or diluting a stock solution.
Conceptual Problems
-
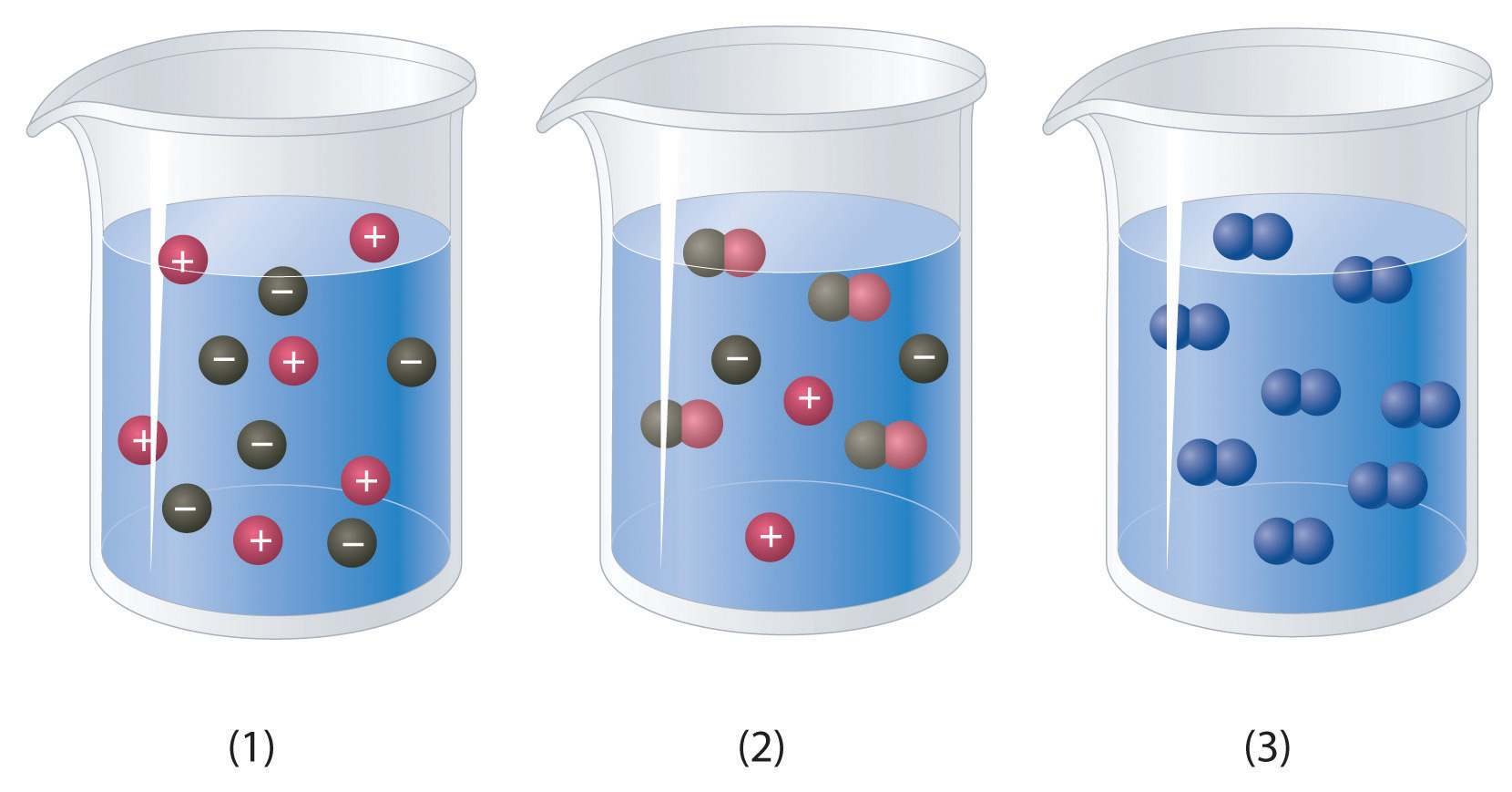
Which of the representations best corresponds to a 1 M aqueous solution of each compound? Justify your answers.
- NH3
- HF
- CH3CH2CH2OH
-
Na2SO4

-
Which of the representations shown in Problem 1 best corresponds to a 1 M aqueous solution of each compound? Justify your answers.
- CH3CO2H
- NaCl
- Na2S
- Na3PO4
- acetaldehyde
-
Would you expect a 1.0 M solution of CaCl2 to be a better conductor of electricity than a 1.0 M solution of NaCl? Why or why not?
-
An alternative way to define the concentration of a solution is molality, abbreviated m. Molality is defined as the number of moles of solute in 1 kg of solvent. How is this different from molarity? Would you expect a 1 M solution of sucrose to be more or less concentrated than a 1 m solution of sucrose? Explain your answer.
-
What are the advantages of using solutions for quantitative calculations?
Answer
-
a) NH3 is a weak base, which means that some of the molecules will accept a proton from water molecules causing them to dissociate into H+ and -OH ions. The H+ ion will associate with the NH3 to form NH4+. Thus this would look the most like beaker #2. b) HF is a weak acid even though F is strongly electronegative. This is because the H-F molecule can form strong hydrogen bonds with the water molecules and remain in a covalent bond that is harder to dissociate. Thus, beaker #2 is also a good choice for this molecule, as only some of the H-F will dissociate to H3O+ and F- ions. c) CH3CH2CH2OHis a covalent compound and will not dissociate to any appreciable extent, thus, beaker #3 is the correct choice. d) Na2SO4 is a soluble ionic compound and will fully dissociate into ions looking most like beaker #1.
-
Yes, because when CaCl2 dissociates it will form 3 ions (1 Ca2+ and 2 Cl– ions) whereas NaCl will only dissociate into 2 ions (Na+ and a Cl–) for each molecule. Thus, CaCl2 will generate more ions per mole than 1 mole of NaCl and be a better conductor of electricity.
-
If the amount of a substance required for a reaction is too small to be weighed accurately, the use of a solution of the substance, in which the solute is dispersed in a much larger mass of solvent, allows chemists to measure the quantity of the substance more accurately.
Numerical Problems
-
Calculate the number of grams of solute in 1.000 L of each solution.
- 0.2593 M NaBrO3
- 1.592 M KNO3
- 1.559 M acetic acid
- 0.943 M potassium iodate
-
Calculate the number of grams of solute in 1.000 L of each solution.
- 0.1065 M BaI2
- 1.135 M Na2SO4
- 1.428 M NH4Br
- 0.889 M sodium acetate
-
If all solutions contain the same solute, which solution contains the greater mass of solute?
- 1.40 L of a 0.334 M solution or 1.10 L of a 0.420 M solution
- 25.0 mL of a 0.134 M solution or 10.0 mL of a 0.295 M solution
- 250 mL of a 0.489 M solution or 150 mL of a 0.769 M solution
-
Complete the following table for 500 mL of solution.
Compound Mass (g) Moles Concentration (M) calcium sulfate 4.86 acetic acid 3.62 hydrogen iodide dihydrate 1.273 barium bromide 3.92 glucose 0.983 sodium acetate 2.42 -
What is the concentration of each species present in the following aqueous solutions?
- 0.489 mol of NiSO4 in 600 mL of solution
- 1.045 mol of magnesium bromide in 500 mL of solution
- 0.146 mol of glucose in 800 mL of solution
- 0.479 mol of CeCl3 in 700 mL of solution
-
What is the concentration of each species present in the following aqueous solutions?
- 0.324 mol of K2MoO4 in 250 mL of solution
- 0.528 mol of potassium formate in 300 mL of solution
- 0.477 mol of KClO3 in 900 mL of solution
- 0.378 mol of potassium iodide in 750 mL of solution
-
What is the molar concentration of each solution?
- 8.7 g of calcium bromide in 250 mL of solution
- 9.8 g of lithium sulfate in 300 mL of solution
- 12.4 g of sucrose (C12H22O11) in 750 mL of solution
- 14.2 g of iron(III) nitrate hexahydrate in 300 mL of solution
-
What is the molar concentration of each solution?
- 12.8 g of sodium hydrogen sulfate in 400 mL of solution
- 7.5 g of potassium hydrogen phosphate in 250 mL of solution
- 11.4 g of barium chloride in 350 mL of solution
- 4.3 g of tartaric acid (C4H6O6) in 250 mL of solution
-
Give the concentration of each reactant in the following equations, assuming 20.0 g of each and a solution volume of 250 mL for each reactant.
- BaCl2(aq) + Na2SO4(aq) →
- Ca(OH)2(aq) + H3PO4(aq) →
- Al(NO3)3(aq) + H2SO4(aq) →
- Pb(NO3)2(aq) + CuSO4(aq) →
- Al(CH3CO2)3(aq) + NaOH(aq) →
-
An experiment required 200.0 mL of a 0.330 M solution of Na2CrO4. A stock solution of Na2CrO4 containing 20.0% solute by mass with a density of 1.19 g/cm3 was used to prepare this solution. Describe how to prepare 200.0 mL of a 0.330 M solution of Na2CrO4 using the stock solution.
-
Calcium hypochlorite [Ca(OCl)2] is an effective disinfectant for clothing and bedding. If a solution has a Ca(OCl)2 concentration of 3.4 g per 100 mL of solution, what is the molarity of hypochlorite?
-
Phenol (C6H5OH) is often used as an antiseptic in mouthwashes and throat lozenges. If a mouthwash has a phenol concentration of 1.5 g per 100 mL of solution, what is the molarity of phenol?
-
If a tablet containing 100 mg of caffeine (C8H10N4O2) is dissolved in water to give 10.0 oz of solution, what is the molar concentration of caffeine in the solution?
-
A certain drug label carries instructions to add 10.0 mL of sterile water, stating that each milliliter of the resulting solution will contain 0.500 g of medication. If a patient has a prescribed dose of 900.0 mg, how many milliliters of the solution should be administered?
Answers
-
a. 39.13 g b. 161.0 g c. 93.57 g d. 201.8 g
-
a. 1.40 L of a 0.334 M solution, b. 25.0 mL of a 0.134 M solution, c. 150 mL of a 0.769 M solution
-
a. 0.815 M, b. 2.09 M, c. 0.182 M, d. 0.684 M
-
a. 0.174 M, b. 0.297 M, c. 0.048 M, d. 0.135 M
-
a. BaCl2 = 0.384 M, Na2SO4 = 0.563 M, b. Ca(OH)2 = 1.08 M, H3PO4 = 0.816 M, c. Al(NO3)3 = 0.376 M, H2SO4 = 0.816 M, d. Pb(NO3)2 = 0.242 M, CuSO4 = 0.501 M, e. Al(CH3CO2) = 0.392 M, NaOH = 2.00 M
-
0.48 M ClO−
-
1.74 × 10−3 M caffeine
(Back to the Top)
8.10 References
- Chung (Peter) Chieh (2016) Inorganic Chemistry. Libretexts. Available at: https://chem.libretexts.org/Core/Inorganic_Chemistry/Chemical_Reactions/Chemical_Reactions_1/Solutions
- Ball, D.W., Hill, J.W., and Scott, R.J. (2016) MAP: The Basics of General, Organic and Biological Chemistry. Libre Texts. Available at: https://chem.libretexts.org/Textbook_Maps/Introductory_Chemistry_Textbook_Maps/Map%3A_The_Basics_of_GOB_Chemistry_(Ball_et_al.)
- Averill, B.A., Eldredge, P. (2012) The Principles of Chemistry. Libre Texts. Available at: https://2012books.lardbucket.org/books/principles-of-general-chemistry-v1.0/index.html
- Hydrate. (2017, August 30). In Wikipedia, The Free Encyclopedia. Retrieved 16:20, September 26, 2017, from https://en.wikipedia.org/w/index.php?title=Hydrate&oldid=798015169
- Lower, S. (2010). Solutions 1: Solutions and their concentrations. In the Online textbook, “Chem1 Virtual Textbook”. Available at: http://www.chem1.com/acad/webtext/solut/solut-1.html
-
OpenStax, Chemistry. OpenStax CNX. Jun 20, 2016 http://cnx.org/contents/85abf193-2bd2-4908-8563-90b8a7ac8df6@9.311.
- Open Textbooks for Hong Kong. (2015) Tonicity chapter from Concepts in Biology. retrieved on Dec 31st, 2018 from http://www.opentextbooks.org.hk/ditatopic/34633
- Rice University () Section 3.1 The Cell Membrane from Anatomy and Physiology. BC Open Textbook Collection. Retreived on Dec 31st, 2018 from https://opentextbc.ca/anatomyandphysiology/chapter/the-cell-membrane/
- Kahn Academy (2019) Homeostasis. In Human Body Systems. Retrieved on Jan 2nd, 2019 from https://www.khanacademy.org/science/high-school-biology/hs-human-body-systems/hs-body-structure-and-homeostasis/a/homeostasis
- Lumen Learning (2019) Homeostasis from Boundless Anatomy and Physiology. Retrieved on Jan 2nd, 2019 from https://courses.lumenlearning.com/boundless-ap/chapter/homeostasis/
- Wikipedia contributors. (2019, February 9). Hypothermia. In Wikipedia, The Free Encyclopedia. Retrieved 18:47, February 25, 2019, from https://en.wikipedia.org/w/index.php?title=Hypothermia&oldid=882437028