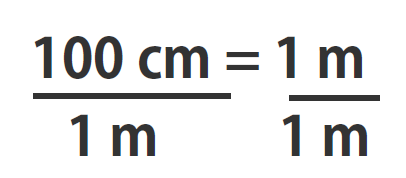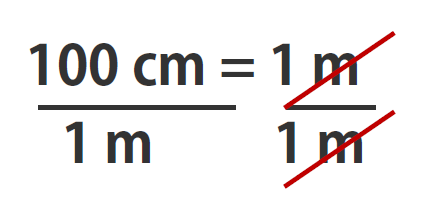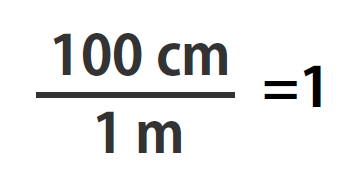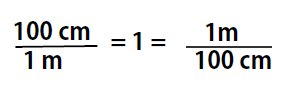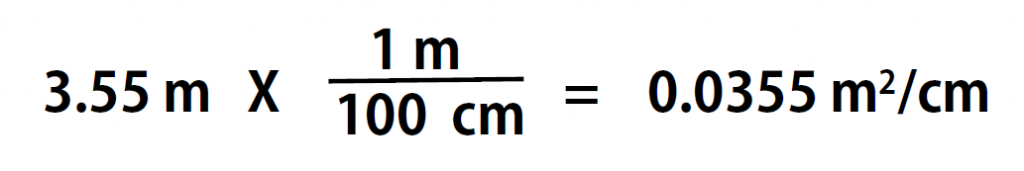Home » Student Resources » Online Chemistry Textbooks » Foundations in General, Organic, and Biological Chemistry » Chapter 1: Measurements in Chemistry
MenuFoundations in General, Organic, and Biological Chemistry
Chapter 1 – Measurements in Chemistry
This content can also be downloaded as an printable PDF or an interactive PDF. For the interactive PDF, adobe reader is required for full functionality.
This text is published under creative commons licensing, for referencing and adaptation, please click here.
Sections:
Section 1: Chemistry and Matter
What is Chemistry?
Physical and Chemical Properties
Elements and Compounds
Mixtures
States of Matter
Section 2: How Scientists Study Chemistry
The Scientific Method
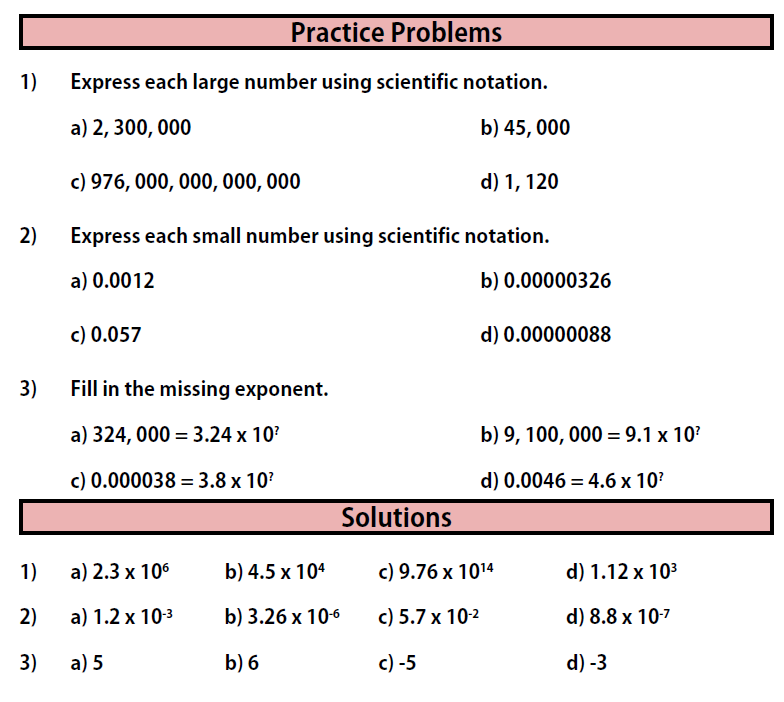
Section 3: Scientific Notation
Video Tutorial
Practice Problems
Section 4: Units of Measurement
International System of Units and the Metric System
Derived SI Units
Section 5: Making Measurements in the Lab
Precision vs. Accuracy
Significant Figures
Exact Numbers
Rules of Rounding
Video Tutorial
Calculations with Significant Figures
Conversions and the Importance of Units
Conversion Factors
Chapter Summary
References
Section 1: Chemistry and Matter
What is Chemistry?
Everything around us is made up of chemicals. From the color that makes a rose so red to the gasoline that fills our cars and the silicon chips that power our computers and cell phones…Chemistry is everywhere! Understanding how chemical molecules form and interact to create complex structures enables us to harness the power of chemistry and use it, just like a toolbox, to create many of the modern advances that we see today. This includes advances in medicine, communication, transportation, building infrastructure, food science and agriculture, and nearly every other technical field that you can imagine.
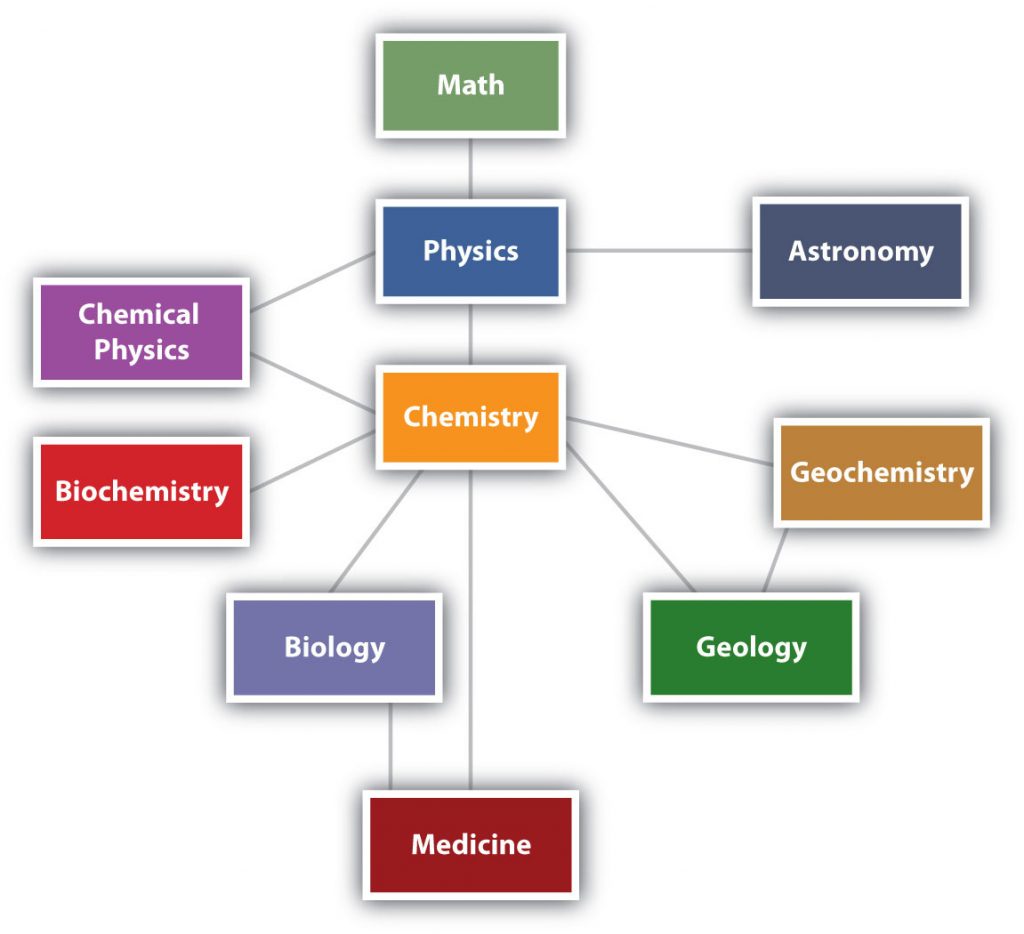
Chemistry is one branch of science. Science is the process by which we learn about the natural universe by observing, testing, and then generating models that explain our observations. is the process by which we learn about the natural universe by observing, testing, and then generating models that explain our observations. Because the physical universe is so vast, there are many different branches of science (Figure 1.1). Thus, chemistry is the study of matter, biology is the study of living things, and geology is the study of rocks and the earth. Mathematics is the language of science, and we will use it to communicate some of the ideas of chemistry.
Although we divide science into different fields, there is much overlap among them. For example, some biologists and chemists work in both fields so much that their work is called biochemistry. Similarly, geology and chemistry overlap in the field called geochemistry. Figure 1.1 shows how many of the individual fields of science are related.
Figure 1.1: The Relationships Between Some of the Major Branches of Science. Chemistry lies more or less in the middle, which emphasizes its importance to many branches of science.
Physical vs. Chemical Properties
Part of understanding matter is being able to describe it. One way chemists describe matter is to assign different kinds of properties to different categories. The properties that chemists use to describe matter fall into two general categories. Physical properties are characteristics that describes matter, such as boiling point, melting point and color. Physical Changes, such as melting a solid into a liquid, do not alter the chemical structure of that matter. Chemical properties are characteristics that describe how the chemical structure of matter changes during a chemical reaction. An example of a chemical property is flammability—a materials ability to burn—because burning (also known as combustion) changes the chemical composition of a material.
Elements and Compounds
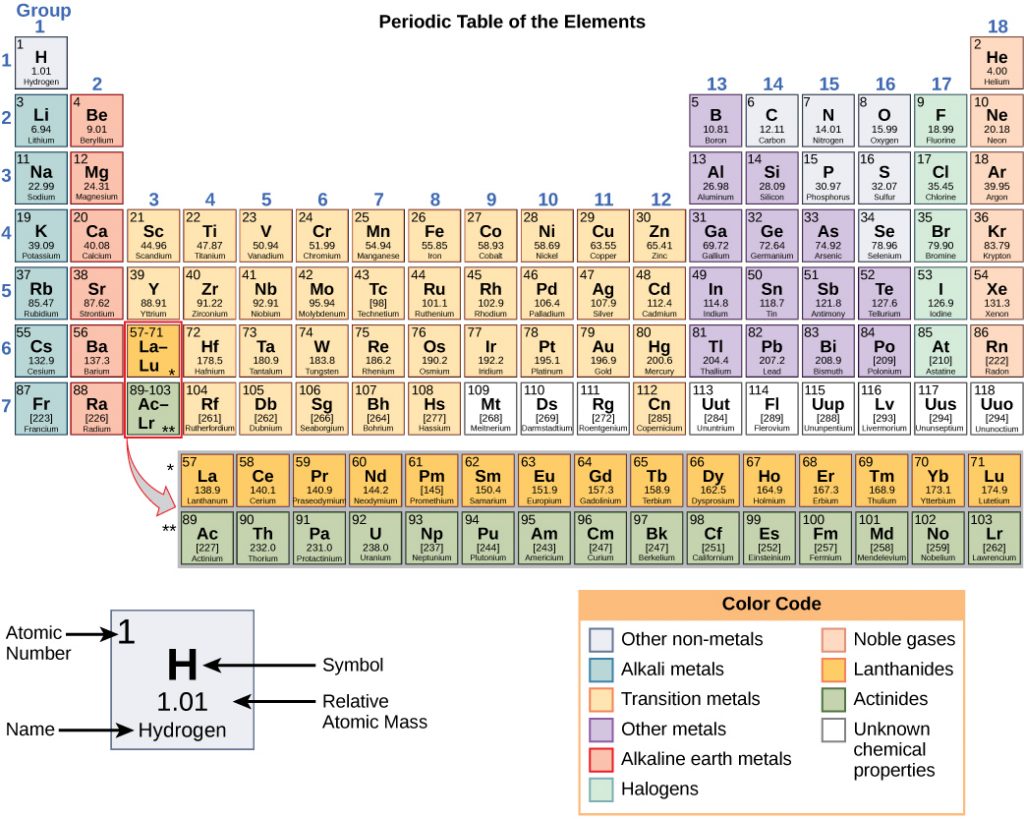
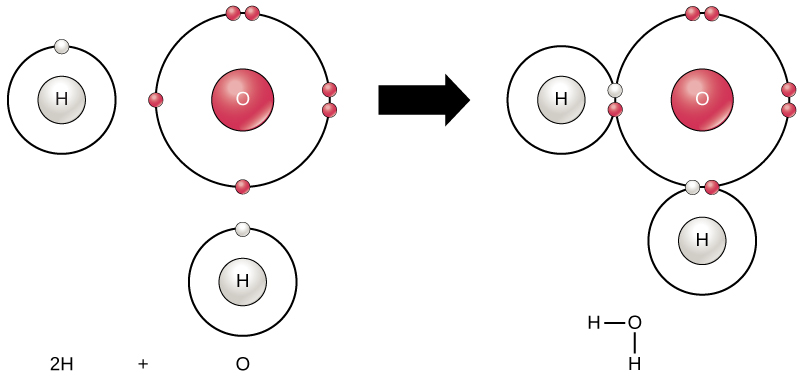
Any sample of matter that has the same physical and chemical properties throughout the sample is called a substance. There are two types of substances. A substance that cannot be broken down into chemically simpler components is an element. Aluminum, which is used in soda cans, is an element. A substance that can be broken down into chemically simpler components (because it has more than one element) is a compound. Water is a compound composed of the elements hydrogen and oxygen. Today, there are about 118 elements in the known universe which are organized on a fundamental chart called the Periodic Table of Elements (Fig. 1.2). In contrast, scientists have identified tens of millions of different compounds to date.
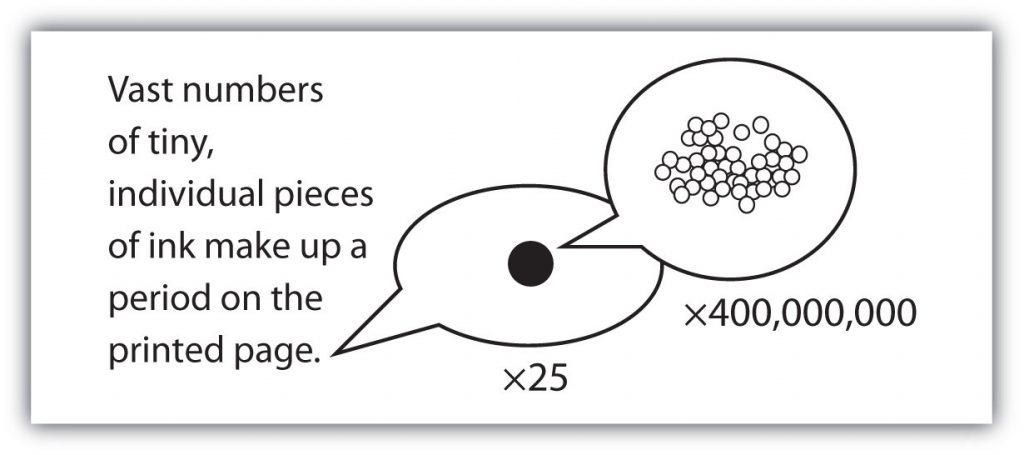
The smallest part of an element that maintains the identity of that element is called an atom. Atoms are extremely tiny; to make a line 1 inch long, you would need 217 million iron atoms! Similarly, the smallest part of a compound that maintains the identity of that compound is called a molecule. Molecules are composed of atoms that are attached together and behave as a unit (Fig. 1.2). Scientists usually work with millions of atoms and molecules at a time. When a scientist is working
Figure 1.2: (Upper Panel) The Periodic Table of the Elements is an organized chart that contains all of the known chemical elements. (Lower Panel) To the left of the arrow is shown one atom of oxygen and two atoms of hydrogen. Each of these represent single elements. When they are combined on the righthand side, they form a single molecule of water (H2O). Note that water is defined as a compound, because each single molecule is made up of more than one type of element, in this case, one atom of oxygen with two atoms of hydrogen.
with large numbers of atoms or molecules at a time, the scientist is studying the macroscopic view of the universe. However, scientists can also describe chemical events on the level of individual atoms or molecules, which is referred to as the microscopic viewpoint. We will see examples of both macroscopic and microscopic viewpoints throughout this book (Figure 1.3).
Figure 1.3: How many molecules are needed for a period in a sentence? Although we do not notice it from a macroscopic perspective, matter is composed of microscopic particles so tiny that billions of them are needed to make a speck that we can see with the naked eye. The X25 and X400,000,000 indicate the number of times the image is magnified.
Mixtures
A material composed of two or more substances is a mixture. In a mixture, the individual substances maintain their chemical identities. Many mixtures are obvious combinations of two or more substances, such as a mixture of sand and water. Such mixtures are called heterogeneous mixtures. In some mixtures, the components are so intimately combined that they act like a single substance even though they are not. Mixtures with a consistent composition throughout are called homogeneous mixtures Homogeneous mixtures that are mixed so thoroughly that neither component can be observed independently of the other are called solutions. Sugar dissolved in water is an example of a solution. A metal alloy, such as steel, is an example of a solid solution. Air, a mixture of mainly nitrogen and oxygen, is a gaseous solution.
Figure 1.4: Heterogeneous vs. Homogeneous Mixtures. A mixture contains more than one substance. In the upper panel you see an example of a heterogeneous mixture of oil and water. The mixture is heterogeneous because you can visibly see two different components in the mixture. In the lower panel, you see an example of a homogeneous mixture, coffee. It is homogeneous because you cannot distinguish the many different components that make up a cup of coffee (water; caffeine; coffee alkaloids and tannins). It looks the same throughout. If the mixture is homogeneous and is also see through or clear, it is called a solution. In our example, the coffee is a solution; however, a concentrated espresso may be very opaque and would only be homogeneous mixture, not a solution.
States of Matter
Another way to classify matter is to describe it as a solid, a liquid, or a gas, which was done in the examples of solutions, above. These three descriptions, each implying that the matter has certain physical properties, represent the three phases of matter. A solid has a definite shape and a definite volume. Liquids have a definite volume but not a definite shape; they take the shape of their containers. Gases have neither a definite shape nor a definite volume, and they expand to fill their containers. We encounter matter in each phase every day. In fact, we regularly encounter water in all three phases: ice (solid), water (liquid), and steam (gas).
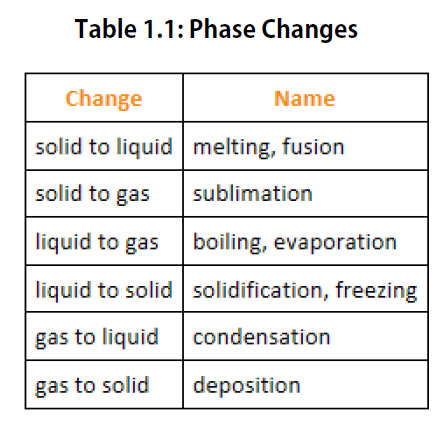
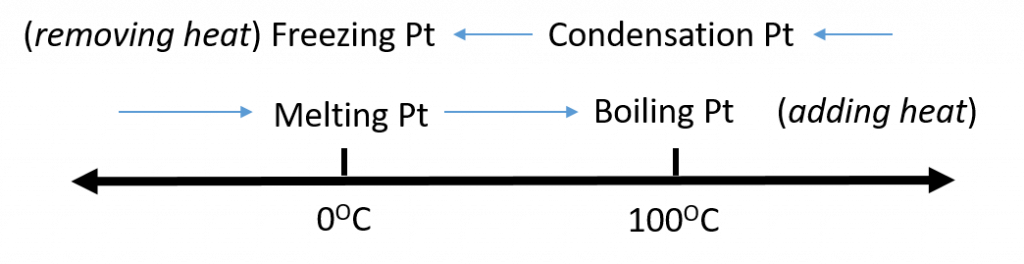
We know from our experience with water that substances can change from one phase to another if the conditions are right. Typically, varying the temperature of a substance (and, less commonly, the pressure exerted on it) can cause a phase change or a physical process in which a substance goes from one phase to another (Figure 1.5). Phase changes have particular names depending on what phases are involved, as summarized in Table 1.1.
Figure 1.5. Analyzing Phase Changes. (Upper panel) A photo of boiling water demonstrates the phase change of water from the liquid to the gaseous phase. Note that phase changes are a physical property of a molecule. The water is still chemically the same (H2O) in the solid, liquid, or gaseous state. (Lower panel) Change in temperature can cause phase changes . Above is the temperature scale for the phase changes of water. If you add heat to solid ice, water will melt at 0oC and boil at 100oC. If you remove heat from gaseous water, it will condense into the liquid state at 100oC and freeze at 0oC.
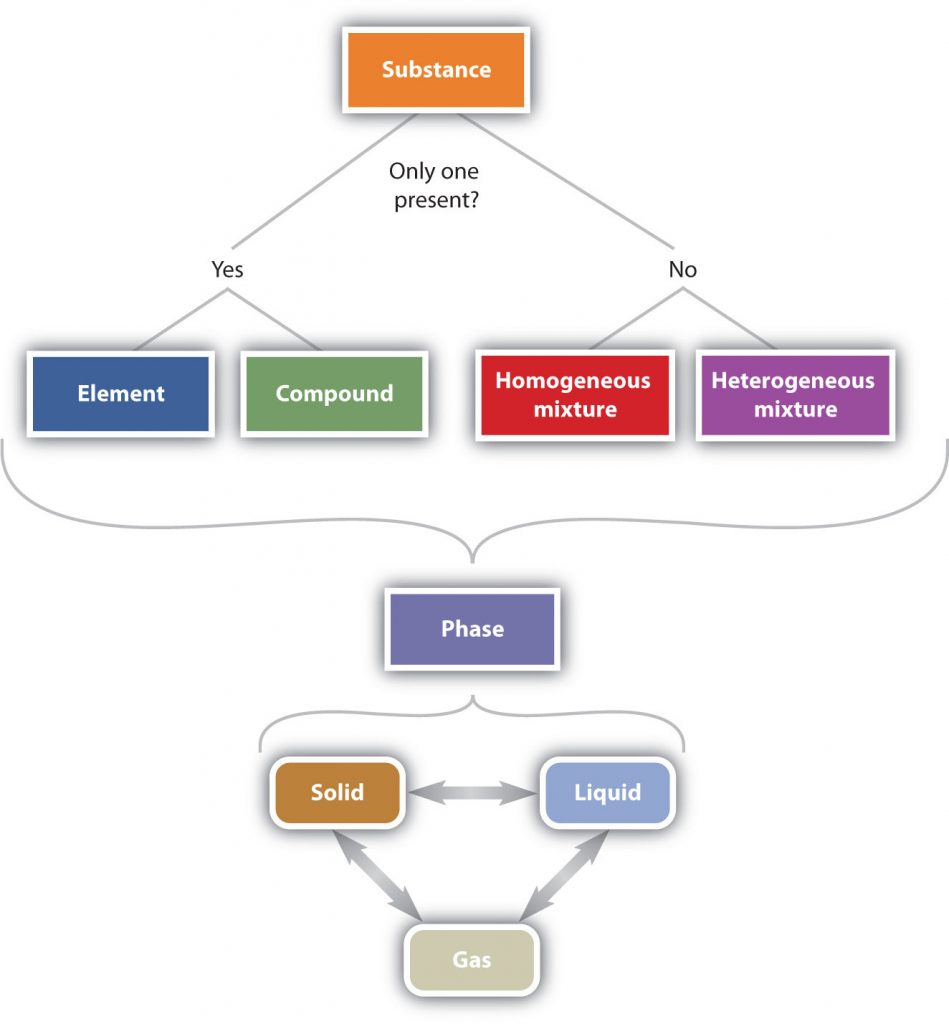
In summary, Figure 1.6 “The Classification of Matter” illustrates the relationships between the different ways matter can be classified.
Figure 1.6 The Classification of Matter. Matter can be classified in a variety of ways depending on its properties
Section 2: How Scientists Study Chemistry
The Scientific Method
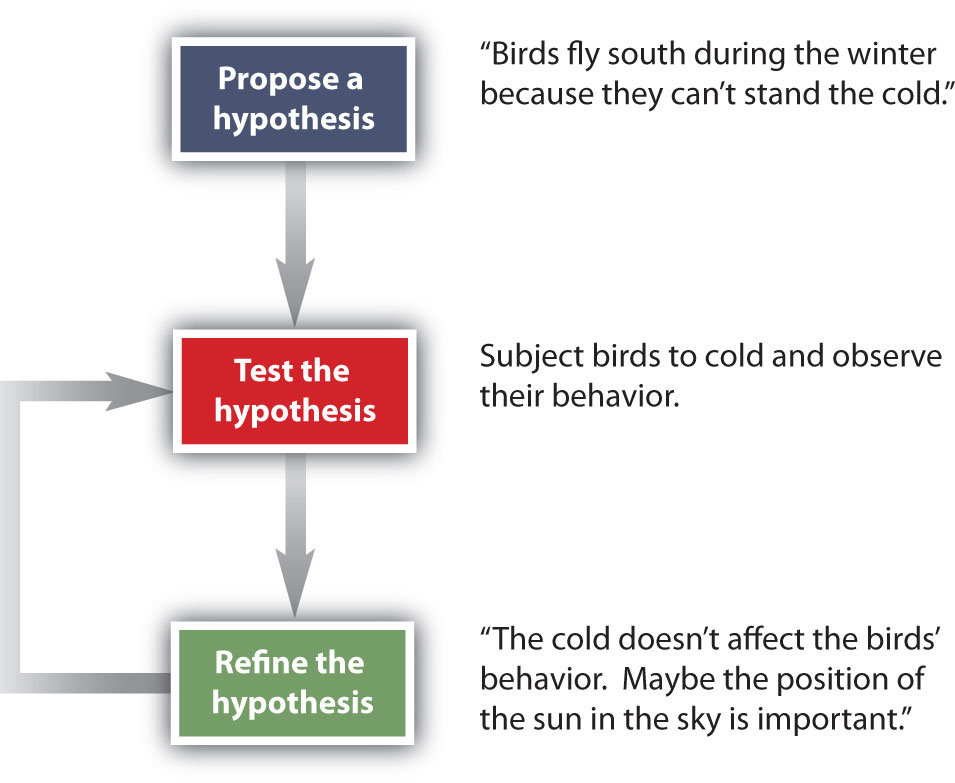
How do scientists work? Generally, they follow a process called the scientific method. The scientific method is an organized procedure for learning answers to questions. To find the answer to a question (for example, “Why do birds fly toward Earth’s equator during the cold months?”), a scientist goes through the following steps, which are also illustrated in Figure 1.7.
Figure 1.7 The General Steps of the Scientific Method. The steps may not be as clear-cut in real life as described here, but most scientific work follows this general outline.
Propose a hypothesis. A scientist generates a testable idea, or hypothesis, to try to answer a question or explain how the natural universe works. Some people use the word theory in place of hypothesis, but the word hypothesis is the proper word in science. For scientific applications, the word theory is a general statement that describes a large set of observations and data. A theory represents the highest level of scientific understanding, and is built from a wide array of factual knowledge or data.
Test the hypothesis. A scientist evaluates the hypothesis by devising and carrying out experiments to test it. If the hypothesis passes the test, it may be a proper answer to the question. If the hypothesis does not pass the test, it may not be a good answer.
Refine the hypothesis if necessary. Depending on the results of experiments, a scientist may want to modify the hypothesis and then test it again. Sometimes the results show the original hypothesis to be completely wrong, in which case a scientist will have to devise a new hypothesis.
Not all scientific investigations are simple enough to be separated into these three discrete steps. But these steps represent the general method by which scientists learn about our natural universe.
Section 3: Scientific Notation
The study of chemistry can involve numbers that are very large. It can also involve numbers that are very small. Writing out such numbers and using them in their long form is problematic, because we would spend far too much time writing zeroes, and we would probably make a lot of mistakes! There is a solution to this problem. It is called scientific notation.
Scientific notation allows us to express very large and very small numbers using powers of 10.
Recall that:
100 = 1 101 = 10 102 = 100
103 = 1000 104 = 10000 105 = 100000
As you can see, the power to which 10 is raised is equal to the number of zeroes that follow the 1. This will be helpful for determining which exponent to use when we express numbers using scientific notation.
Let us take a very large number:
579, 000, 000, 000
and express it using scientific notation.
First, we find the coefficient, which is a number between 1 and 10 that will be multiplied by 10 raised to some power.
Our coefficient is: 5.79
This number will be multiplied by 10 that is raised to some power. Now let us figure out what power that is.
We can do this by counting the number of positions that stand between the end of the original number and the new position of the decimal point in our coefficient.
5 . 7 9 0 0 0 0 0 0 0 0 0
↑ ↑
How many positions are there?
We can see that there are 11 positions between our decimal and the end of the original number. This means that our coefficient, 5.79, will be multiplied by 10 raised to the 11th power.
Our number expressed in scientific notation is:
5.79 x 1011
But what about very small numbers?
You may recall that:
10-1 = 0.1 10-2 = 0.01 10-3 = 0.001
10-4 = 0.0001 10-5 = 0.00001
The number of spaces to the right of the decimal point for our 1 is equal to the number in the exponent that is behind the negative sign. This is useful to keep in mind when we express very small numbers in scientific notation.
Here is a very small number:
0.0000642
Let us express this number using scientific notation.
Our coefficient will be 6.42
This number will be multiplied by 10 raised to some power, which will be negative. Let us figure out the correct power. We can figure this out by counting how many positions stand between the decimal point in our coefficient and the decimal point in our original number.
0 . 0 0 0 0 6 4 2
↑ ↑
How many positions?
There are 5 positions between our new decimal point and the decimal point in the original number, so our coefficient will be multiplied by 10 raised to the negative 5th power.
Our number written in scientific notation is:
6.42 x 10-5
You can use these methods to express any large or small number using scientific notation.
VIDEO TUTORIAL FOR SIGNIFICANT FIGURES:
Section 4: Units of Measurement
International System of Units and the Metric System
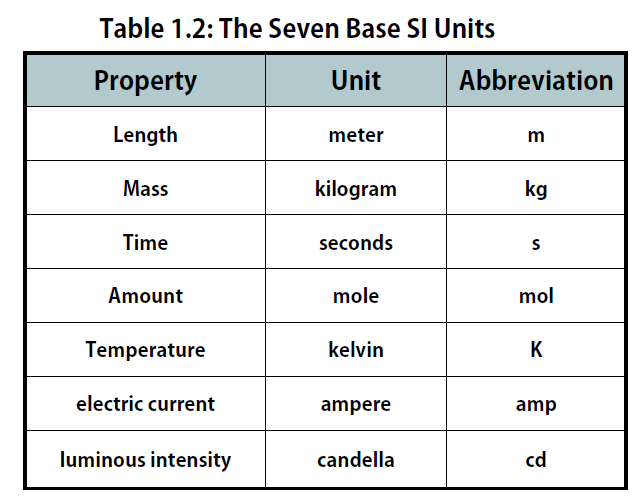
The International System of Units, abbreviated SI from the French Système International D’unités, is the main system of measurement units used in science. Since the 1960s, the International System of Units has been internationally agreed upon as the standard metric system. The SI base units are based on physical standards. The definitions of the SI base units have been and continue to be modified and new base units added as advancements in science are made. Each SI base unit except the kilogram is described by stable properties of the universe.
There are seven base units, which are listed in Table 1.2. Chemistry primarily uses five of the base units: the mole for amount, the kilogram for mass, the meter for length, the second for time, and the kelvin for temperature. The degree Celsius (oC) is also commonly used for temperature. The numerical relationship between kelvins and degrees Celsius is as follows
K = oC + 273
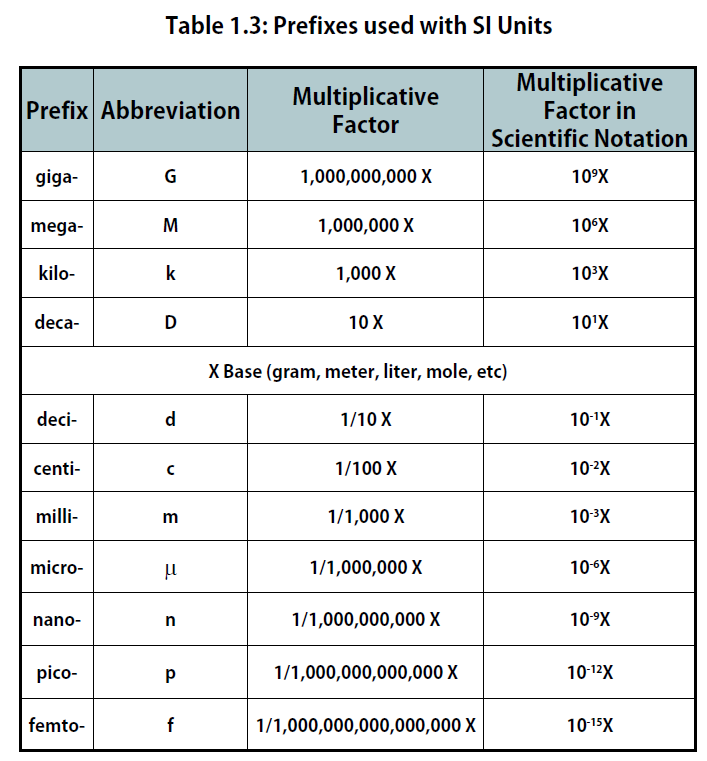
The size of each base unit is defined by international convention. For example, the kilogram is defined as the quantity of mass of a special metal cylinder kept in a vault in France (Figure 1.8). The other base units have similar definitions. The sizes of the base units are not always convenient for all measurements. For example, a meter is a rather large unit for describing the width of something as narrow as human hair. Instead of reporting the diameter of hair as 0.00012 m or even 1.2 × 10-4 m, SI also provides a series of prefixes that can be attached to the units, creating units that are larger or smaller by powers of 10, known as the metric system.
Figure 1.8 The Kilogram. The standard for the kilogram is a platinum-iridium cylinder kept in a speacial vault in France. Source: Wikimedea (https://commons.wikimedia.org/wiki/File:National_prototype_kilogram_K20_replica.jpg)
Common prefixes and their multiplicative factors are listed in Table 1.3 “Prefixes Used with SI Units”. (Perhaps you have already noticed that the base unit kilogram is a combination of a prefix, kilo- meaning 1,000 ×, and a unit of mass, the gram.) Some prefixes create a multiple of the original unit: 1 kilogram equals 1,000 grams (or 1 kg = 1,000 g), and 1 megameter equals 1,000,000 meters (or 1 Mm = 1,000,000 m). Other prefixes create a fraction of the original unit. Thus, 1 centimeter equals 1/100 of a meter, 1 millimeter equals 1/1,000 of a meter, 1 microgram equals 1/1,000,000 of a gram, and so forth.
The basic unit of mass in the International System of Units is the kilogram. A kilogram is equal to 1000 grams. A gram is a relatively small amount of mass and so larger masses are often expressed in kilograms. When very tiny amounts of matter are measured, we often use milligrams which are equal to 0.001 gram. There are numerous larger, smaller, and intermediate mass units that may also be appropriate. At the end of the 18th century, a kilogram was the mass of a liter of water. In 1889, a new international prototype of the kilogram was made of a platinum-iridium alloy. The kilogram is equal to the mass of this international prototype, which is held in Paris, France.
Mass and weight are not the same thing. Although we often use the terms mass and weight interchangeably, each one has a specific definition and usage. The mass of an object is a measure of the amount of matter in it. The mass (amount of matter) of an object remains the same regardless of where the object is placed. For example, moving a brick to the moon does not cause any matter in it to disappear or be removed.
The weight of an object is determined by the force that gravitation exerts upon the object. The weight is equal to the mass of the object times the local acceleration of gravity. Thus, on the Earth, weight is determined by the force of attraction between the object and the Earth. Since the force of gravity is not the same at every point on the Earth’s surface, the weight of an object is not constant. The gravitational pull on the object varies depending on where the object is with respect to the Earth or other gravity-producing object. For example, a man who weighs 180 pounds on Earth would weigh only 45 pounds if he were in a stationary position, 4,000 miles above the Earth’s surface. This same man would weigh only 30 pounds on the moon because the moon’s gravity is only one-sixth that of Earth. The mass of this man, however, would be the same in each situation. For scientific experiments, it is important to measure the mass of a substance rather than the weight to retain consistency in the results regardless of where you are performing the experiment.
Length
The SI unit of length is the meter. In 1889, the definition of the meter was a bar of platinum-iridium alloy stored under conditions specified by the International Bureau of Standards. In 1960, this definition of the standard meter was replaced by a definition based on a wavelength of krypton-86 radiation. In 1983, that definition was replaced by the following: the meter is the length of the path traveled by light in a vacuum during a time interval of a second.
Temperature
When used in a scientific context, the words heat and temperature do NOT mean the same thing. Temperature represents the average kinetic energy of the particles that make up a material. Increasing the temperature of a material increases its thermal energy. Thermal energy is the sum of the kinetic and potential energy in the particles that make up a material. Objects do not “contain” heat; rather they contain thermal energy. Heat is the movement of thermal energy from a warmer object to a cooler object. When thermal energy moves from one object to another, the temperature of both objects change.
A thermometer is a device that measures temperature. The name is made up of “thermo” which means heat and “meter” which means to measure. The temperature of a substance is directly proportional to the average kinetic energy it contains. In order for the average kinetic energy and temperature of a substance to be directly proportional, it is necessary that when the temperature is zero, the average kinetic energy must also be zero. It was necessary for use in calculations in science for a third temperature scale in which zero degrees corresponds with zero kinetic energy, that is, the point where molecules cease to move. This temperature scale was designed by Lord Kelvin. Lord Kelvin stated that there is no upper limit of how hot things can get, but there is a limit as to how cold things can get. In 1848, William Lord Kelvin developed the idea of absolute zero, which is the temperature at which molecules stop moving and therefore, have zero kinetic energy. This is known as the Kelvin temperature scale.
The Celcius scale is based on the freezing point and boiling point of water. Thus, 0oC is the freezing point of water, whereas 100oC is the boiling point of water. Most of us are familiar with temperatures that are below the freezing point of water. It should be apparent that even though the air temperature may be -5oC, the molecules of air are still moving (i.e. 0oC is not absolute zero). Substances like oxygen gas and nitrogen gas have already melted and boiled to vapor at temperatures below -150oC.
The Fahrenheit scale is also defined by the freezing point and boiling points of water. However, the scale is different from that of the Kelvin and Celsius scales. In the Fahrenheit scale, the freezing point of water is 32oF and the boiling point of water is 212oF. To convert between the Fahrenheit scale and the Celsius scale , the following conversions can be used:
[oC] = ([oF] -32) × 5/9 or [oF] = [oC] × 9/5 + 32
The Kelvin temperature scale has its zero at absolute zero (determined to be -273.15oC), and uses the same degree scale as the Celsius scale. Therefore, the mathematical relationship between the Celsius scale and the Kelvin scale is
K = oC + 273.15
In the case of the Kelvin scale, the degree sign is not used. Temperatures are expressed simply as 450 K, and are always positive.
Time
The SI unit for time is the second. The second was originally defined as a tiny fraction of the time required for the Earth to orbit the Sun. It has since been redefined several times. The definition of a second (established in 1967 and reaffirmed in 1997) is: the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium-133 atom.
Amount
Chemists use the term mole to represent a large number of atoms or molecules. Just as a dozen implies 12 things, a mole (mol) represents 6.022 × 1023 things. The number 6.022 × 1023, called Avogadro’s number after the 19th-century chemist Amedeo Avogadro, is the number we use in chemistry to represent macroscopic amounts of atoms and molecules. Thus, if we have 6.022 × 1023 Oxygen atoms, we say we have 1 mol of Oxygen atoms. If we have 2 mol of Na atoms, we have 2 × (6.022 × 1023) Na atoms, or 1.2044 × 1024 Na atoms. Similarly, if we have 0.5 mol of benzene (C6H6) molecules, we have 0.5 × (6.022 × 1023) C6H6 molecules, or 3.011 × 1023 C6H6 molecules.
Derived SI Units
Derived units are combinations of SI base units. Units can be multiplied and divided, just as numbers can be multiplied and divided. For example, the area of a square having a side of 2 cm is 2 cm × 2 cm, or 4 cm2 (read as “four centimeters squared” or “four square centimeters”). Notice that we have squared a length unit, the centimeter, to get a derived unit for area, the square centimeter.
Volume
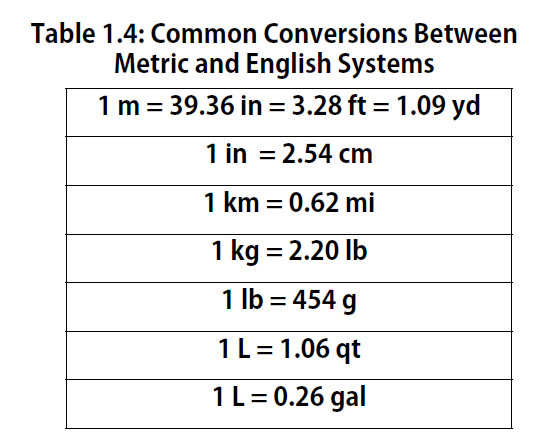
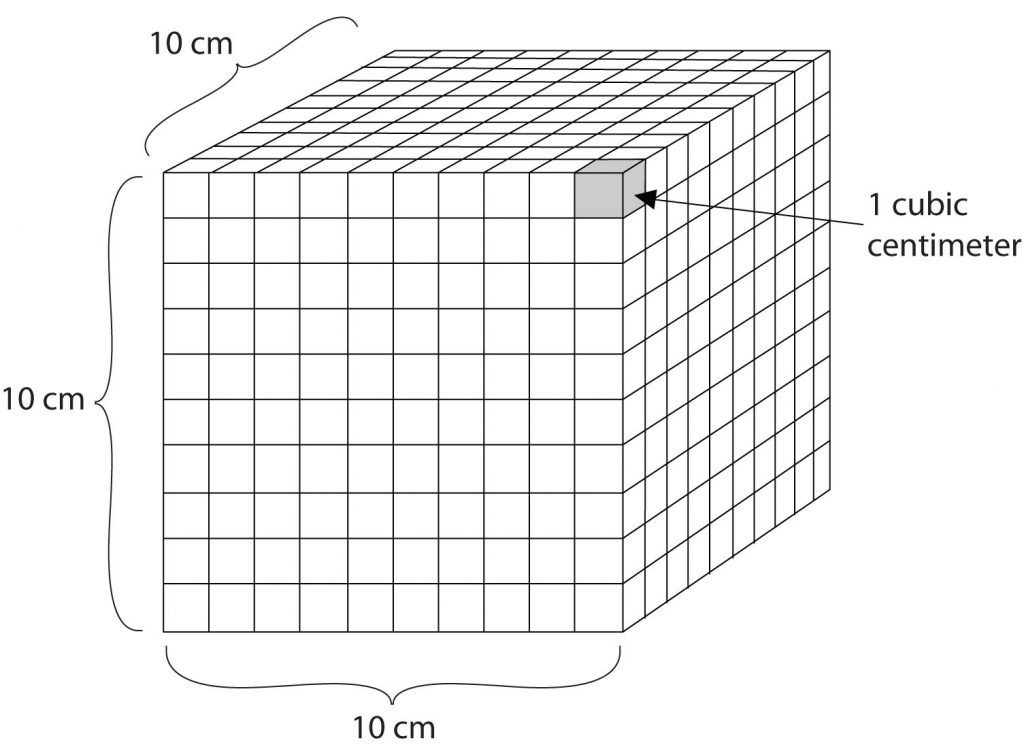
Volume is an important quantity that uses a derived unit. Volume is the amount of space that a given substance occupies and is defined geometrically as length × width × height. Each distance can be expressed using the meter unit, so volume has the derived unit m × m × m, or m3 (read as “meters cubed” or “cubic meters”). A cubic meter is a rather large volume, so scientists typically express volumes in terms of 1/1,000 of a cubic meter. This unit has its own name—the liter (L). A liter is a little larger than 1 US quart in volume. (Table 1.4) gives approximate equivalents for some of the units used in chemistry.) As shown in Figure 1.9 “The Liter”, a liter is also 1,000 cm3. By definition, there are 1,000 mL in 1 L, so 1 milliliter and 1 cubic centimeter represent the same volume.
1 mL = 1 cm3
Figure 1.9: The Liter. A liter is defined as a cube that is 10 cm (1/10th of a meter) on a side. A milliliter, 1/1000th of a liter, is equal to 1 cubic centimeter (1 cm3).
Energy
Energy, another important quantity in chemistry, is the ability to perform work. Moving a box of books from one side of a room to the other side, for example, requires energy. It has a derived unit of kg·m2/s2. (The dot between the kg and m2 units implies the units are multiplied together and then the whole term is divided by s2.) Because this combination is cumbersome, this collection of units is redefined as a joule (J), which is the SI unit of energy. An older unit of energy, the calorie (cal), is also widely used. There are:
4.184 J = 1 cal
Note that this differs from our common use of the big ‘Calorie’or ‘Cal’ listed on food packages in the United States. The big ‘Cal’ is actually a kilocalorie or kcal (Fig 1.10) Note that all chemical processes or reactions occur with a simultaneous change in energy and that energy can be stored in chemical bonds.
Figure 1.10: The Difference between kilocalories in Scientific and Common Use. Calories represented on food packaging actually refer to kilocalories in scientific terms.
Density
Density is defined as the mass of an object divided by its volume; it describes the amount of matter contained in a given amount of space.
density=mass/volume
Thus, the units of density are the units of mass divided by the units of volume: g/cm3 or g/mL (for solids and liquids, respectively), g/L (for gases), kg/m3, and so forth. For example, the density of water is about 1.00 g/mL, while the density of mercury is 13.6 g/mL. Mercury is over 13 times as dense as water, meaning that it contains over 13 times the amount of matter in the same amount of space. The density of air at room temperature is about 1.3 g/L.
Section 5: Making Measurements in the Lab
Precision vs. Accuracy
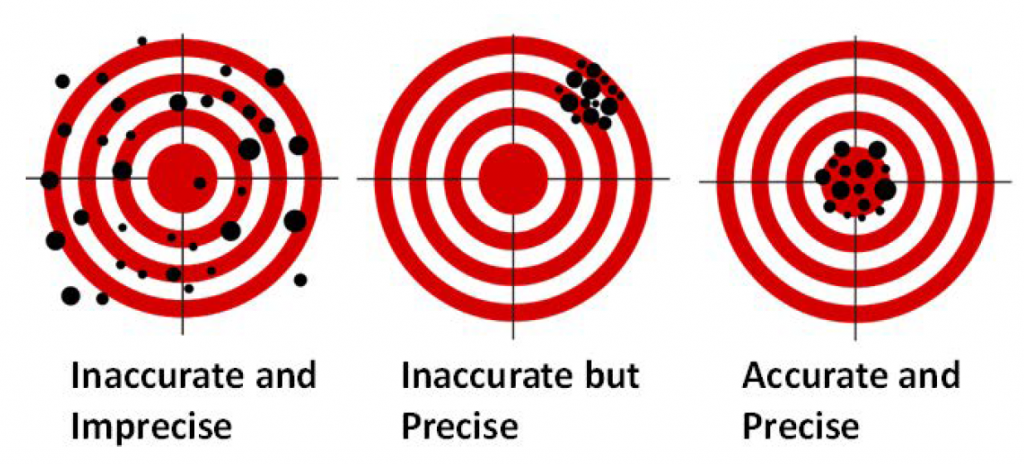
It is important to note the different terminology we use when talking in science. One such set of terminology is precision and accuracy. Although precision and accuracy are often used interchangeably in the non-scientific community, the difference between the terms is extremely important to realize. Precision tells you how close two measurements are to one another, while accuracy tells you how close a measurement is to the known value. A measurement can be precise while not being accurate, or accurate but not precise; the two terms are NOT related. A good analogy can be found in a game of darts (Fig. 1.11). A player who always hits the same spot just to the left of the dart board would be precise but not very accurate. However, a dart player who is all over the board but hits the center of the board on average would be accurate but not precise. A good darts player, just like a good scientist, wants to be both precise and accurate.
Figure 1.11: Difference Between Accuracy and Precision. A game of darts can be used to show the difference between accuracy and precision.
Adapted from: https://upload.wikimedia.org/wikipedia/commons/thumb/5/5d/Reliability_and_validity.svg/717px-Reliability_and_validity.svg.png
Typically within the laboratory, accuracy is a measure of how well your equipment is calibrated. For example, if your balance is not calibrated correctly, you can make very precise, repeated measurements, but the measurements will not represent the true value. Precision, on the otherhand, is usually determined by how careful the scientist is in making measurements. If you are careless and spill part of your sample on the way, your measurements in repeated experiments will not be precise even if your balance is accurate.
Significant Figures
It is important to realize that values in scientific measurements are never 100% accurate. Our instruments only measure to a certain level of accuracy. Thus, we can pick different instruments to make a measurement based upon the level of accuracy we need for the experiment. Due to the inherent inaccuracy in any measured number we must keep track of the different levels of accuracy each number has with significant figures. Significant figures of a measured quantity are defined as all the digits known with certainty and the first uncertain, or estimated, digit. It makes no sense to report any digits after the first uncertain one, so it is the last digit reported in a measurement. Zeros are used when needed to place the significant figures in their correct positions. Thus, zeros may or may not be significant figures. Significant figures apply in the real world, as they allow us to quantify the accuracy of any type of measurement. To identify how many numbers in a measurement have significance, you can follow a discreet set of rules, shown below and to the right.
Figure 1.12: Measuring an Object to the Correct Number of Significant Figures.
How many digits should be shown in this measurement?
The correct answer is 3! The two that you know for sure + the estimated position…for this reading it would be close to 1.37
Exact Numbers
Exact numbers are numbers that are not measured by a scientific instrument. They are either used as definitions to define a concept or terminology, or they are made by counting the total of something present. An example of an exact number, would be the number of eggs in a carton or a defined unit such as there are 100 cm in 1 m. Exact numbers, such as the number of people in a room, DO NOT affect the number of significant figures in calculations made with measured values.
Rules of Rounding
In scientific operations, the rules of rounding may be a little bit different than the ones you are used to using. Normal rounding rules suggest that if a number is 4 or below, it should be rounded down to the lower number, whereas if it is 5 or higher, it should be rounded up. However, note that 5 is right in the middle and causes a problem when using these conventional rounding rules. If you have a large dataset of numbers that you need to round, using this rounding rule will lead to bias in your dataset (i.e. 4/9th of the time you will be rounding down, and 5/9th of the time you will be rounding up). In a large dataset, this bias is unacceptable.
In Scientific Rounding, we typically use a rule called ‘Rounding to the Even.’ In this rounding system the rules are the same for 4 and below, you round down to the lower number, and for 6 and above you round up to the higher number. However, if the number you are rounding is 5, then you round to the even number. This helps to alleviate the sample bias that can occur when rounding large datasets.
Calculations with Significant Figures
The first thing to realize before performing any calculations in science is that all measured numbers are only as good as the instrument used to measure them. Even with the best instrument available the measured number will never be 100% exact. Scientists use the “good enough” rule of precision, meaning that we accept an inherent amount of imprecision from every measurement we take as long as the final result is close enough to where we want it to be. This concept becomes dangerous when we begin to use these “good enough” numbers for any calculations, if we aren’t careful to keep track of our significant figures our numbers can quickly lose their “good enough” status. To protect their “good enough” numbers, the scientific community has set forth certain rules for performing any calculations; in this section we need only concern ourselves with two very important rules: the Addition/Subtraction rule, and the Multiplication/Division rule.
Addition/Subtraction Rule:
- Find the number with the least number of decimals and keep track of the number of decimal places
- Perform the addition/subtraction
- Round the final answer to the least number of decimals found in Step 1
Multiplication/Division Rule:
- Count the number of significant figures in each number (keep track of the number of significant figures)
- Perform the multiplication/division
- Round your final answer to the lowest number of significant figures found in step 1
Calculating Complicated Problems:
- Using the order of operations, break the problem up into multiple steps
- Perform any addition/subtraction steps following the Addition/Subtraction rule (Do not round yet, just keep track of the correct number of decimals when finding the number of significant figures)
- Perform multiplication/division using the Multiplication/Division rule
- Round the final answer to the correct number of significant figures
Conversions and the Importance of Units
The ability to convert from one unit to another is an important skill. For example, a nurse with 50 mg aspirin tablets who must administer 0.2 g of aspirin to a patient, needs to know that 0.2 g equals 200 mg, so that 4 tablets are needed. Fortunately, there is a simple way to convert from one unit to another.
Conversion Factors
If you learned the SI units and prefixes described in Section 1.4 Units of Measurement”, then you know that 1 cm is 1/100th of a meter or:
100 cm = 1 m
Suppose we divide both sides of the equation by 1 m (both the number and the unit; Note that it is critically important to always write out your units! This avoids confusion and mistakes when making conversions.):
As long as we perform the same operation on both sides of the equals sign, the expression remains an equality. Look at the right side of the equation; it now has the same quantity in the numerator (the top) as it has in the denominator (the bottom). Any fraction that has the same quantity in the numerator and the denominator has a value of 1:
We know that 100 cm is 1 m, so we have the same quantity on the top and the bottom of our fraction, although it is expressed in different units. A fraction that has equivalent quantities in the numerator and the denominator but expressed in different units is called a conversion factor
Note that conversion factors can be written with either term in the numerator or denominator, and used as appropriate for the problem that you want to solve. This is because, both terms are equal to 1
Here is a simple example. How many centimeters are there in 3.55 m? Perhaps you can determine the answer in your head. If there are 100 cm in every meter, then 3.55 m equals 355 cm. To solve the problem more formally with a conversion factor, we first write the quantity we are given, 3.55 m. Then we multiply this quantity by a conversion factor, which is the same as multiplying it by 1. We can write 1 as 100cm/1m and multiply:
Because m, the abbreviation for meters, occurs in both the numerator and the denominator of our expression, they cancel out. The final step is to perform the calculation that remains once the units have been canceled. Note that it is CRITICAL to retain the right units in the final answer or it will not make sense. A generalized description of this process is as follows:
quantity (old units) × conversion factor = quantity (new units)
You may be wondering why we use a seemingly complicated procedure for a straightforward conversion. In later studies, the conversion problems you will encounter will not always be so simple. If you can master the technique of applying conversion factors, you will be able to solve a large variety of problems.
In the previous example, we used the fraction 100 cm/1 m as a conversion factor. Does the conversion factor 1 m/100 cm also equal 1? Yes, it does; it has the same quantity in the numerator as in the denominator (except that they are flip-flopped). Why did we not use that conversion factor? If we had used the second conversion factor, the original unit would not have canceled, and the result would have been meaningless. Here is what we would have gotten:
INCORRECT USE OF CONVERSION FACTOR!!
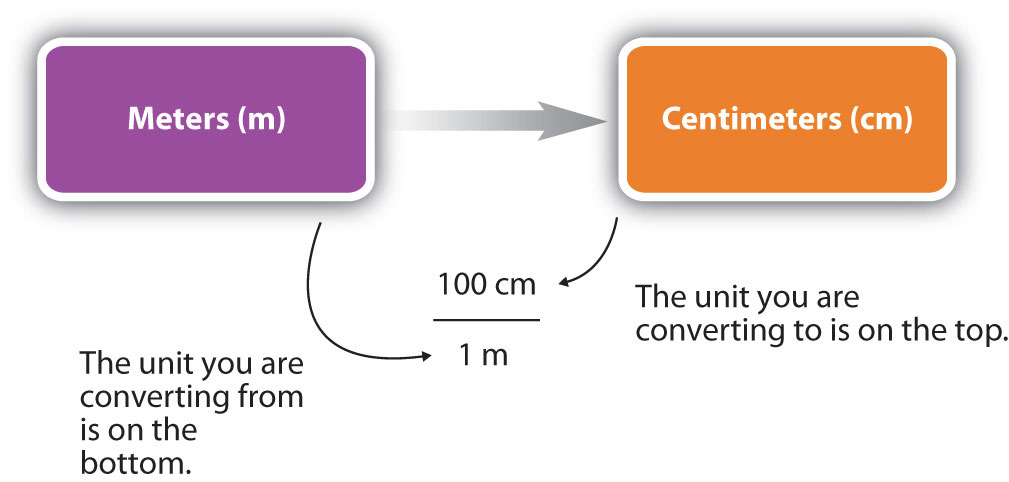
You can see that none of the units cancelled out. For the answer to be meaningful, we have to construct the conversion factor in a form that causes the original unit to cancel out. Figure 1.13 “A Concept Map for Conversions” shows a concept map for constructing a proper conversion.
Figure 1.13 A Concept Map for Conversions. This is how you construct a conversion factor to convert from one unit to another.
Chapter Summary
References:
Chapter 1 materials have been adapted and modified from the following creative commons resources unless otherwise noted:
1. Anonymous. (2012) Introduction to Chemistry: General, Organic, and Biological (V1.0). Published under Creative Commons by-nc-sa 3.0. Available at: http://2012books.lardbucket.org/books/introduction-to-chemistry-general-organic-and-biological/index.html
2. Poulsen, T. (2010) Introduction to Chemistry. Published under Creative Commons by-nc-sa 3.0. Available at: http://openedgroup.org/books/Chemistry.pdf
3. OpenStax (2015) Atoms, Isotopes, Ions, and Molecules: The Building Blocks. OpenStax CNX.Available at: http://cnx.org/contents/be8818d0-2dba-4bf3-859a-737c25fb2c99@12.