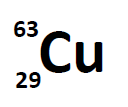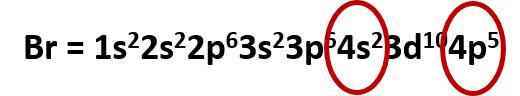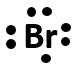Home » Student Resources » Online Chemistry Textbooks » CH104: Chemistry and the Environment » CH104 – Chapter 2: Atoms and The Periodic Table
MenuCH104: Chemistry and the Environment
Chapter 2: Atoms and the Periodic Table
This text is published under creative commons licensing, for referencing and adaptation, please click here.
2.1 Atomic Theory with Historical Perspectives
2.2 Introduction to Elements and the Periodic Table
2.3 Dmitri Mendeleev and the development of the periodic table
2.4 Families of the Periodic Table
2.5 Defining the Atom
Basic Atomic Structure – electrons, neutrons, and protons
2.6 Atomic Number – Protons Determine the Identity of an Element
2.7 Atomic Mass, Isotopes, and Allotropes
2.8 Electronic Structure of Atoms
The Four Electronic Quantum Numbers
Electron Orbital Filling Rules
Electron Configurations and the Periodic Table
Electron Configuration Solitaire
Electron Configuration Shorthand
Electron-Dot Symbols
2.9 Periodic Table Trends
Atomic Size
Electronegativity
Ionization Energy
Metallic and Nonmetallic Character
2.10 Focus on the Environment – Nuclear Energy
Introduction to Radioactivity
Nuclear Fission Reactions and Energy
2.11 Chapter Summary and Homework
2.12 References
2.1 Atomic Theory with Historical Perspectives
What are the smallest building blocks of everyday objects? This is a question that has interested man since the age of the Greek philosophers. Like the ancient Greeks we can perform a simple thought experiment that raises a very important question for modern chemistry: suppose you were given a piece of aluminum foil and asked to cut the foil in half over and over. How long could you continue cutting, assuming that you had no limitations based on your own abilities? Is there a limit on how small matter can be broken up into, or could you infinitely divide matter into smaller and smaller pieces? This argument dates as far back as the Greek philosophers. Most, like Aristotle, argued that matter could be divided infinitely. However, one brilliant philosopher, Democritus, argued that there is a limit. He proposed that the smallest piece that any element (like aluminum) can be divided into and still be recognized as that element is an Atom, a word derived from the Greek word atomos, meaning “indivisible”.
Figure 2.1: Democritus
Photo taken from: Public Domain
Philosophers, like Democritus, based most of their ideas off of thought experiments like the one above instead of actual observations and experimentation. It is for this reason that Democritus’ ideas on atoms were dismissed until 1808, when John Dalton, an English scientist, proposed four fundamental assumptions based upon observations that we call Dalton’s Atomic Theory.
Dalton proposed that:
-
Matter is made up of tiny particles called atoms
-
Atoms cannot be broken into smaller pieces. During a chemical reaction, atoms are rearranged, but they do not break apart, nor are they created or destroyed
-
All atoms of the same element are identical in mass and other properties
-
Atoms of different elements differ in mass and other properties
2.2 Introduction to Elements and the Periodic Table
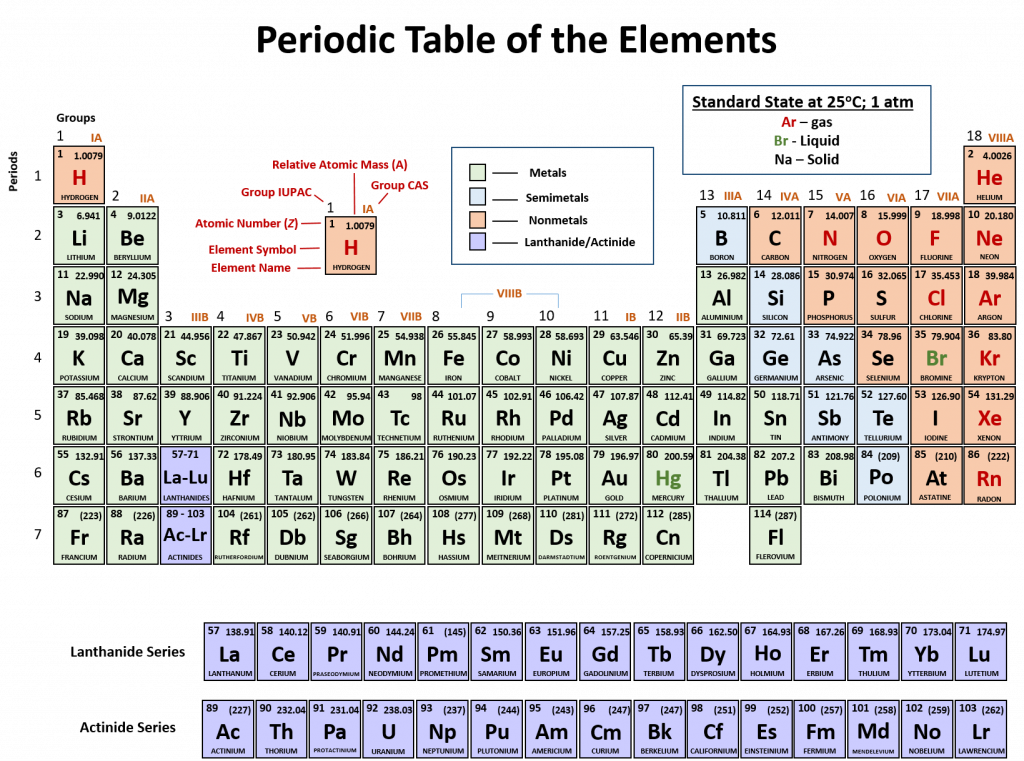
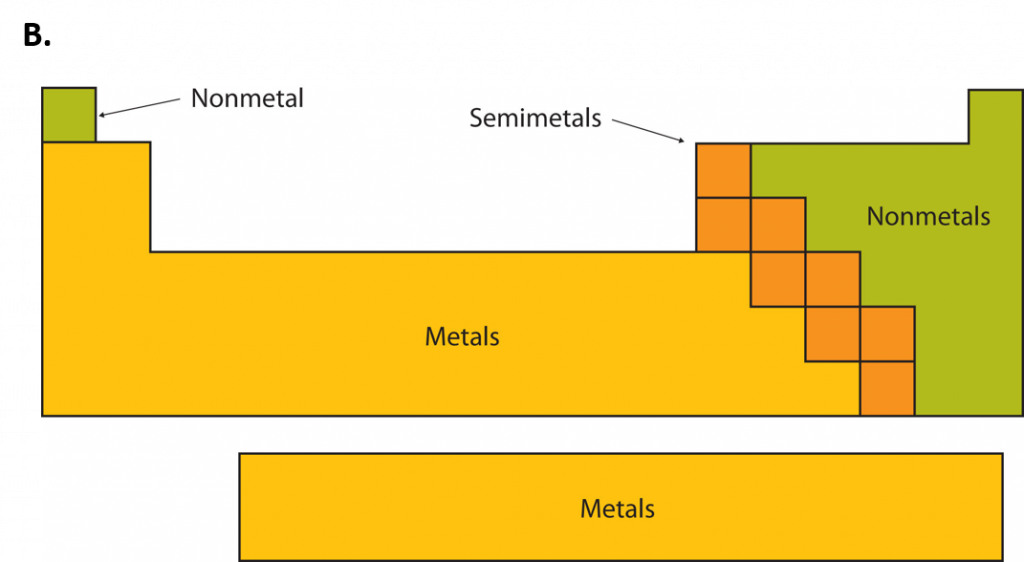
An element is a substance that cannot be broken down into simpler chemical substances. There are about 90 naturally occurring elements known on Earth. Using technology, scientists have been able to create nearly 30 additional elements that are not readily found in nature. Today, chemistry recognizes a total of 118 elements which are all represented on a standard chart of the elements, called the Periodic Table of Elements. Each element is represented by a one or two letter code, where the first letter is always capitalized and, if a second letter is present, it is written in lowercase. For example, the symbol for Hydrogen is H, and the symbol for carbon is C. Some of the elements have seemingly strange letter codes, such as sodium which is Na. These letter codes are derived from latin terminology. For example, the symbol for sodium (Na) is derived from the latin word, natrium, which means sodium carbonate. Elements in the periodic table can be broken up into different general classes based upon similarities in their properties. Going from left to right across the periodic table, the elements can be broken up into metals, metalloids, and nonmetals.
Metals are typically shiny, very dense, and have high melting points. Most metals are ductile (can be drawn out into thin wires), malleable (can be hammered into thin sheets), and good conductors of both heat as well as electricity. All metals are solids at room temperature except for mercury. In chemical reactions, metals easily lose electrons to form positive ions. Examples of metals are silver, gold, and zinc.
Nonmetals are generally brittle, dull, have low melting points, and they are generally poor conductors of heat as well as electricity. In chemical reactions, they tend to gain electrons to form negative ions. Examples of nonmetals are hydrogen, carbon, and nitrogen.
Metalloids have properties of both metals and nonmetals. Metalloids can be shiny or dull. Electricity and heat can travel through metalloids, although not as easily as they can through metals. They are also called semimetals. They are typically semi-conductors, which means that they are elements that conduct electricity better than insulators, but not as well as conductors. They are valuable in the computer chip industry. Examples of metalloids are silicon and boron.
A.
Periodic Table Downloadable PDF Version
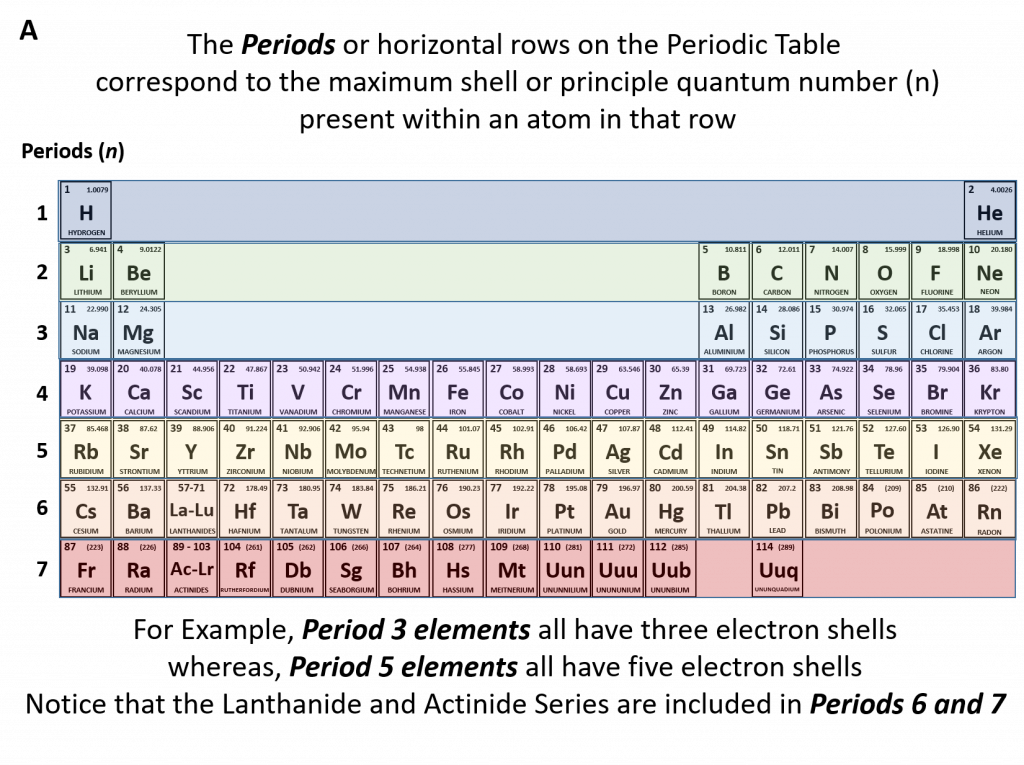
Figure 2.2: Periodic Table of the Elements. All of the known chemical elements are arranged in the format of a table. The table has been set up in such a way that the characteristics of each different element can be predicted by their position on the table. (A) On this rendition of the periodic table, you can see that the pink elements on the lefthand side of the table are the metals, while the blue elements on the right are the non-metals (Hydrogen is the only exception to this rule and will be explained in the subsequent sections). The metalloids (also termed semi-metals) occur in a stairstep pattern between the metals and nonmetals and are represented in this diagram by the green elements. (B) Shows the positions of the metals, nonmetals and metalloids on the periodic table. During this chapter, you will learn more about these unique characteristics, called periodic trends.
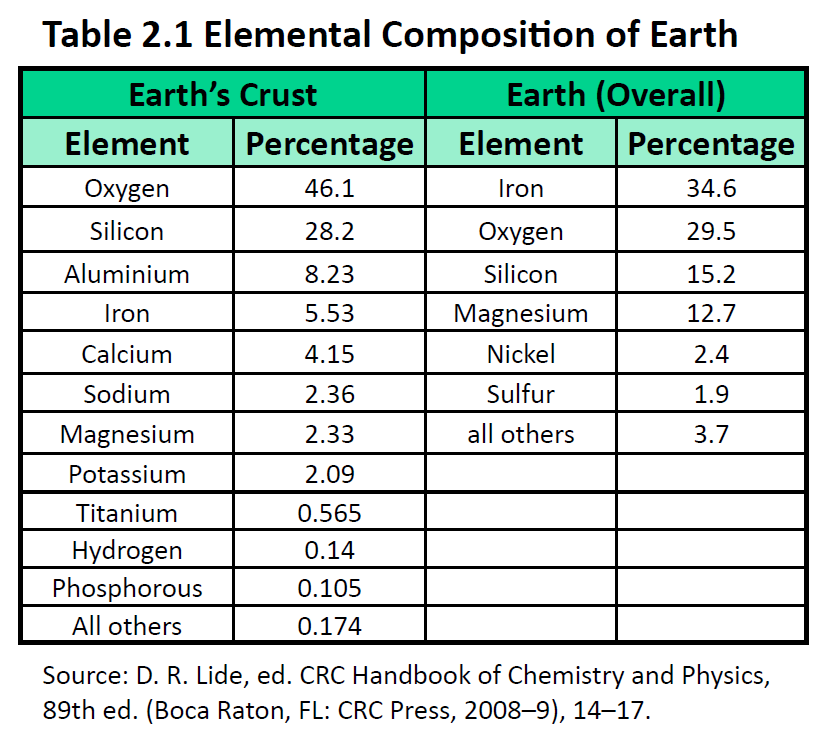
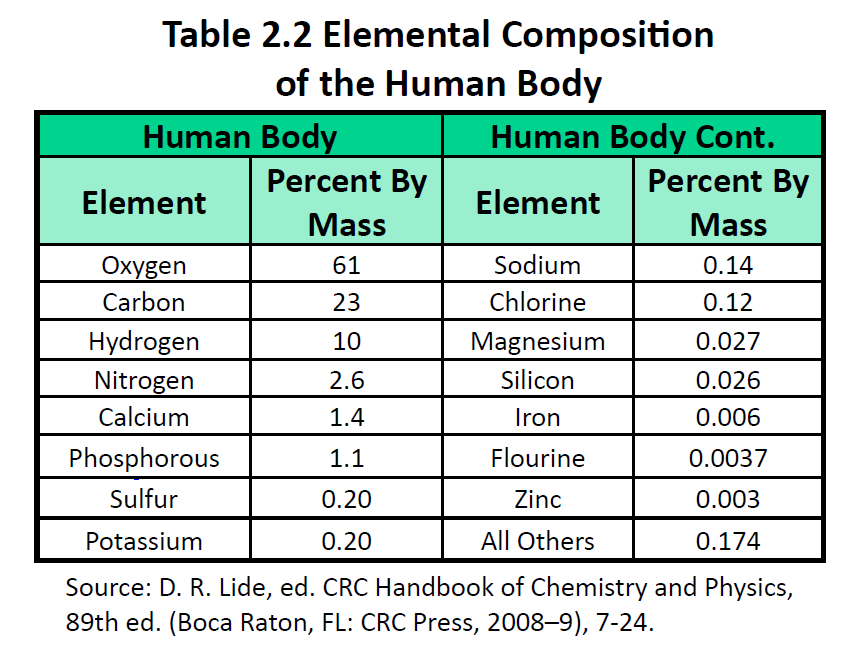
The elements vary widely in abundance. In the universe as a whole, the most common element is hydrogen (about 90%), followed by helium (most of the remaining 10%). All other elements are present in relatively minuscule amounts, as far as we can detect. On the planet Earth, however, the situation is rather different. Oxygen makes up 46.1% of the mass of Earth’s crust (the relatively thin layer of rock forming Earth’s surface), mostly in combination with other elements, while silicon makes up 28.5%. Hydrogen, the most abundant element in the universe, makes up only 0.14% of Earth’s crust. Table 2.1 lists the relative abundances of elements on Earth as a whole and in Earth’s crust. Table 2.2 lists the relative abundances of elements in the human body. If you compare Table 2.1 and 2.2, you will find disparities between the percentage of each element in the human body and on Earth. Oxygen has the highest percentage in both cases, but carbon, the element with the second highest percentage in the body, is relatively rare on Earth and does not even appear as a separate entry in Table 2.1; carbon is part of the 0.174% representing “other” elements. How does the human body concentrate so many apparently rare elements?
The relative amounts of elements in the body have less to do with their abundances on Earth than with their availability in a form we can assimilate. We obtain oxygen from the air we breathe and the water we drink. We also obtain hydrogen from water. On the other hand, although carbon is present in the atmosphere as carbon dioxide, and about 80% of the atmosphere is nitrogen, we obtain those two elements from the food we eat, not the air we breathe.
2.3 Dmitri Mendeleev and the development of the periodic table
In the 19th century, many previously unknown elements were discovered, and scientists noted that certain sets of elements had similar chemical properties. For example, chlorine, bromine, and iodine react with other elements (such as sodium) to make similar compounds. Likewise, lithium, sodium, and potassium react with other elements (such as oxygen) to make similar compounds. Why is this so?
In 1864, Julius Lothar Meyer, a German chemist, organized the elements by atomic mass and grouped them according to their chemical properties. Later that decade, Dmitri Mendeleev, a Russian chemist, organized all the known elements according to similar properties. He left gaps in his table for what he thought were undiscovered elements, and he made some bold predictions regarding the properties of those undiscovered elements. Later, when elements were discovered whose properties closely matched Mendeleev’s predictions, his version of the table gained favor in the scientific community. Because certain properties of the elements repeat on a regular basis throughout the table (that is, they are periodic), it became known as the periodic table.
Figure 2.3: Dmitri Medeleev’s 1871 Early Version of the Periodic Table
Photo of Dmitri Medeleev provided by: кабинет академика Михаила Михайловича Шульца – фото любезно передано мне в собственность вдовой М.М.Шульца Ниной Дмитриевной Шульц
Periodic Table provided by: Den fjättrade ankan
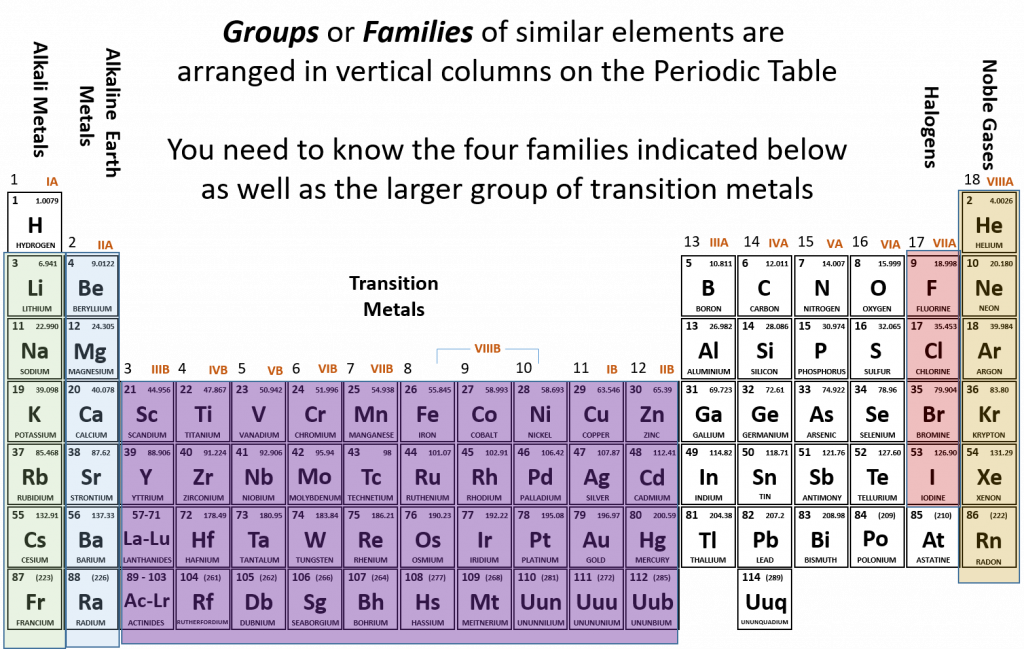
2.4 Families of the Periodic Table
Remember that Mendeleev arranged the periodic table so that elements with the most similar properties were placed in the same group. A group, or family of elements, is a vertical column of the periodic table. Elements are placed into families due to their similar properties, characteristics, and reactivities. For example, all of the elements in group 1 (except for hydrogen, which has unique properties) are very reactive and form compounds in the same ratios and with similar properties as other 1 elements. Due to the similarities in their chemical properties, Mendeleev put these elements into the same group and they came to be known as the alkali metals. The alkali metals include: lithium, sodium, potassium, rubidium, cesium, and francium. Alkali metals are among the most reactive metals. This is due in part to their larger atomic radii and low ionization energies, that will be discussed in more details in section 2.8 below. They get their name from ancient Arabic (al qali) because “scientists” of the time found that the ashes of the vegetation they were burning contained a large amount of sodium and potassium. In Arabic, al qali means ashes. Although most metals tend to be very hard, alkali metals have a soft texture, are silvery in color and can be easily cut. They also have low boiling and melting points and are less dense than most elements. Figure 2.4 shows some of the most common families on the periodic table.
Figure 2.4 Common Families and Groups of the Periodic Table.
The same pattern is true of other vertical groups on the periodic table. Group 2 is called the alkaline earth metals. Once again these elements have similar properties to each other. alkaline earth metals include Beryllium, Magnesium, Calcium, Barium, Strontium and Radium and are soft, silver metals that are less metallic in character than the Group 1 alkali metals. Although many characteristics are common throughout the group, the heavier metals such as Ca, Sr, Ba, and Ra are almost as reactive as the Group 1 alkali metals. They get their name because early “scientists” found that all of the alkaline earth metals were found in the earth’s crust.
The transition metals are the larger block of elements shown in purple on Figure 2.4 extending from Groups 3-12 (also known as the group B elements). Transition elements differ from the main group elements (group A elements) in that they tend to be hard and have high densities. They have high melting points and boiling points and can show various oxidation states when forming chemical bonds (this will be discussed further in chapter 3). They often form colored compounds that are highly stable and they can serve as good catalysts. A catalyst is an agent that helps to speed up a chemical reaction without itself being changed in the process.
Group 17 elements are also called halogens. This group contains very reactive nonmetals. The halogens are an interesting group. Halogens are members of Group 17, which is also referred to as 7A. It is the only group in the Periodic Table that contains all of the states of matter at room temperature. Fluorine, F2 and chlorine, Cl2 are gases, while Bromine, Br2, is a liquid and iodine, I2, and astatine, At, are both solids. Another interesting feature about Group 17 is that it houses four (4) of the seven (7) diatomic elements. Diatomic elements only exist in nature as a pair of atoms of the same element that are bonded together. The seven diatomic elements are H2, N2, O2, F2, Cl2, Br2, and I2. Notice that the latter four are Group 17 elements. The word halogen comes from the Greek meaning salt forming. French chemists discovered that the majority of halogen ions will form salts when combined with metals.
The noble gases are in group 18. The two most significant properties of noble gases is that they are extremely unreactive, rarely forming compounds, and that they all exist as gases at room temperature. We will learn the reason for their unreactivity when we discuss how compounds form in chapters 3 and 4. The first person to isolate a noble gas was Henry Cavendish, who isolated argon in the late 1700s. The noble gases were actually considered inert gases until the 1960s when a compound was formed between xenon and fluorine which changed the way chemists viewed the “inert” gases. In the English language, inert means to be lifeless or motionless; in the chemical world, inert means does not react. Later, the name “noble gas” replaced “inert gas” for the name of Group 18. The elements in this group are also gases at room temperature.
2.5 Defining the Atom
Basic Atomic Structure – electrons, neutrons, and protons
The modern atomic theory, proposed about 1803 by the English chemist John Dalton, is a fundamental concept that states that all elements are composed of atoms. An atom is the smallest part of an element that maintains the identity of that element. Individual atoms are extremely small; even the largest atom has an approximate diameter of only 5.4 × 10−10 m. With that size, it takes over 18 million of these atoms, lined up side by side, to equal the width of your little finger (about 1 cm).
Most elements in their pure form exist as individual atoms. For example, a macroscopic chunk of iron metal is composed, microscopically, of individual iron atoms. Some elements, however, exist as groups of atoms called molecules. Several important elements exist as two-atom combinations and are called diatomic molecules. In representing a diatomic molecule, we use the symbol of the element and include the subscript 2 to indicate that two atoms of that element are joined together. The elements that exist as diatomic molecules are hydrogen (H2), oxygen (O2), nitrogen (N2), fluorine (F2), chlorine (Cl2), bromine (Br2), and iodine (I2).
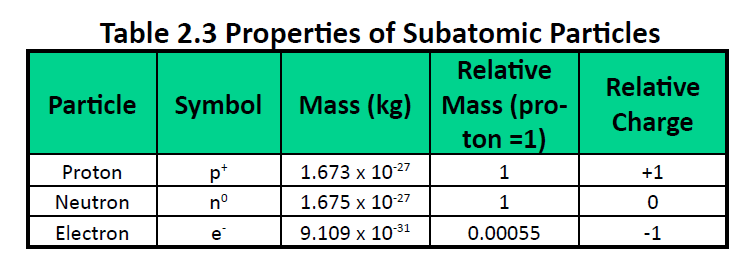
Atoms are made up of extremely small subatomic particles called protons, neutrons, and electrons. Protons are positively charged particles with a relative mass of 1.672622×10-24g, which form part of the core nucleus of an atom. The other part of the atomic nucleus is made up of neutrons, electrically neutral particles with a relative mass almost identical to a proton (1.674927×10-24g). Electrons are extremely small (9.109328×10-28g) negatively charged particles that form an electron cloud, which orbits the nucleus.Table 2.3 summarizes some of the general properties of subatomic particles.
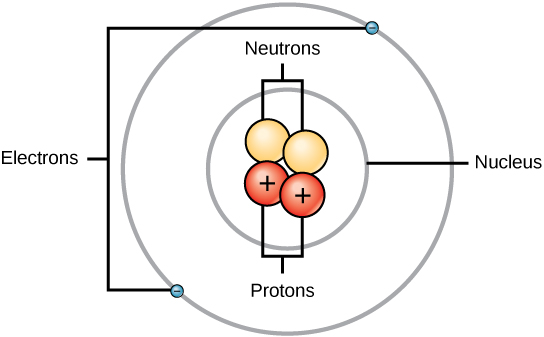
Experiment have shown that protons and neutrons are concentrated in a central region of each atom called the nucleus (plural, nuclei). Electrons are outside the nucleus and orbit about it because they are attracted to the positive charge in the nucleus. Figures 2.5 and 2.6 depict the structure of an atom.
Figure 2.5 The Anatomy of an Atom. The protons and neutrons of an atom are found clustered at the center of the atom in a structure called the nucleus. The electrons orbit the nucleus of the atom within an electron cloud, or the empty space that surrounds the atom’s nucleus. Note that most of the area of an atom is taken up by the empty space of the electron cloud.
Diagram provided by: CNX OpenStax
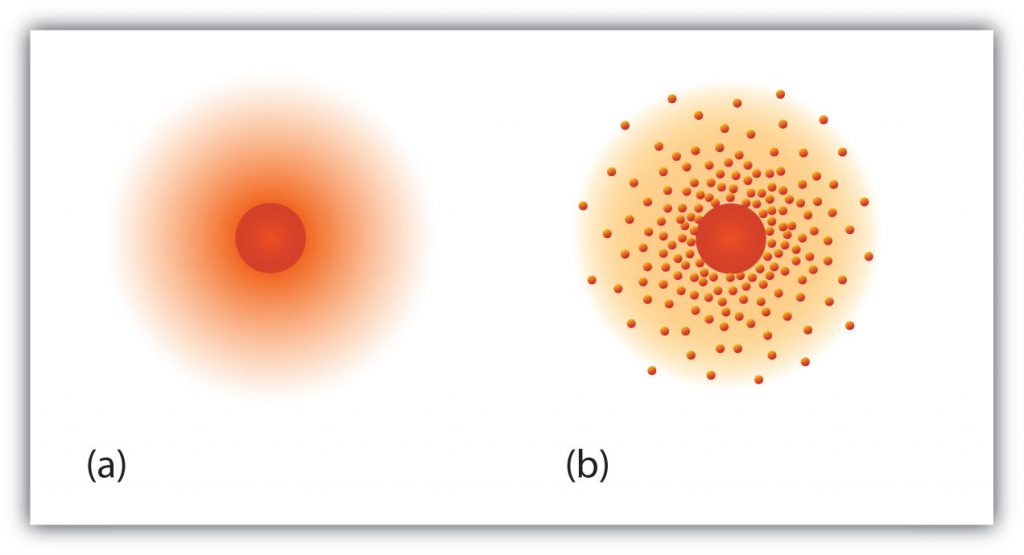
Fig 2.6 The path of the electron in a hydrogen atom. Electrons are not in discrete orbits like planets around the sun. Instead there is a probability that an electron may occupy a certain space within the electron cloud (a) The darker the color, the higher the probability that the hydrogen’s one electron will be at that point at any given time. (b) Similarly, the more crowded the dots, the higher the probability that hydrogen’s one electron will be at that point. In both diagrams, the nucleus is in the center of the diagram.
Most of the mass of an atom is in the nucleus, while the orbiting electrons account for an atom’s size. As a result, an atom consists largely of empty space. Atomic particles are so small that it is impractical to measure them in grams, instead we use a relative mass scale which makes the numbers much more manageable. We use Atomic Mass Units (AMU or u) to measure the mass of atomic particles, one AMU is equal to 1/12th the mass of an atom of carbon-12. You may also see Atomic Mass Units referred to as Daltons (Da) after John Dalton, the English Chemist that first proposed the atomic theory. Carbon-12 has 6 protons and 6 neutrons in its nucleus, meaning that one amu is equal to the average of the masses of a proton and a neutron. The mass of an atom in AMUs is equal to the number of protons and neutrons making up the atom. For example the atomic mass of bromine is roughly 80 amu and its proton number is 35, meaning that bromine has 35 protons and 45 neutrons in its nucleus.
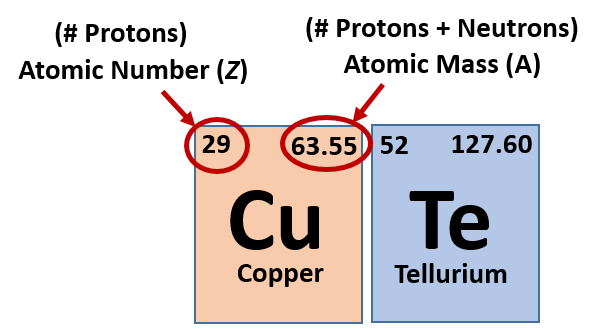
2.6 Atomic Number – Protons Determine the Identity of an Element
When looking at the periodic table you might notice that for each element there are two sets of numbers around the symbol. These symbols correspond to important values that give you important information about each element (Figure 2.7). The most important value corresponding to characteristics of an element is the proton number, which is also called atomic number (represented by the mathematical term, Z). As it turns out, the number of protons that an atom holds in its nucleus is the key determining feature for its chemical properties. In short, an element is defined by the number of protons found in its nucleus. If you refer back to the Periodic Table of Elements shown in figure 2.2, you will see that the periodic table is organized by the number of protons that an element contains. Thus, as you read across each row of the Periodic Table (left to right), each element increases by one proton (or one Atomic Number, Z). When atoms are in their elemental states, their overall charge is zero and the atoms are neutral. Since protons are positively charged and electrons are negatively charged, this means that when atoms are in their elemental form, the number of protons equals the number of electrons. Therefore, if you know the atomic number of an atom, you also know how many electrons are present in that atom when it is in its elemental form. When atoms combine with one another to form compounds, like water (H2O), they will either share or donate/accept electrons from their bonding partners. It is this movement of electrons that facilitates chemical bond formation. Thus, during bond formation the number of electrons around an atom may change, but the atomic number (or number of protons) remains constant and does not change.
Fig 2.7 Structure of the Periodic Table. Each element on the periodic table is represented by the atomic symbol (Cu for Copper, and Te for Tellurium). Sometimes the Atomic Number is written in the upper lefthand corner, and the Atomic Mass in the righthand corner, as shown in this figure. Sometimes, periodic tables will show the atomic number above the element symbol and the atomic mass below the element symbol, as shown in the periodic table in Figure 2.2.
2.7 Atomic Mass, Isotopes, and Allotropes
Atomic mass (A) is the total mass of an atom of a specific element and can be calculated by adding up the number of protons and neutrons present within an atom. The electrons are ignored in the mass calculation because they are so small that they barely add any mass to the atom.
# Protons + # Neutrons = Atomic Mass
Thus, if you know any two of the the three values (atomic mass, atomic number, or number of neutrons), you can calculate the third value. For example, nitrogen has an atomic mass of 14.007 and an atomic number of 7. Thus, it contains 7 protons, and 7 neutrons (14.007 – 7 = 7.007, which is then rounded to 7). Note that the number of neutrons in an atom does not have to equal the number of protons in the atom. For example, lead (Pb), contains 82 protons and has an atomic mass of 207.2. Thus it contains 125 neutrons (207.2 – 82 = 125). Thus, if you know the atomic mass and the atomic number of an element, you can calculate the number of neutrons present, or if you know the atomic mass and the number of neutrons, you can calculate the atomic number.
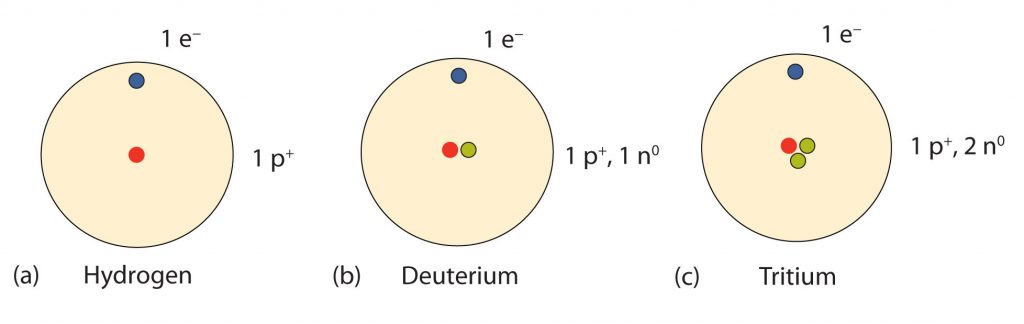
So…how many neutrons are in atoms of a particular element? At first it was thought that the number of neutrons in a nucleus was also defining characteristic of an element. However, it was found that atoms of the same element can have different numbers of neutrons. Atoms of the same element that have different numbers of neutrons are called isotopes. An example of the three common isotopes of hydrogen are shown in Figure 2.8. Note that each of the hydrogen isotopes is known by a unique name, hydrogen, deuterium, and tritium. Not all elemental isotopes have such unique names. Many of the isotopes are distinguished from one another by including the atomic mass in the definition. For example, 99% of the carbon atoms on Earth have 6 neutrons and 6 protons in their nuclei, this is known as carbon-12; just under 1% of the carbon atoms have 7 neutrons and 6 protons in their nuclei, which is known as carbon-13, and an even smaller percent is carbon with 8 neutrons and 6 protons, or carbon-14. Carbon-14 is unstable and will decay over time making it a radioactive form of carbon. The half-life of carbon, or the time it takes for half of the isotope to breakdown is 5,700 years. Overall, there are 15 known isotopes of carbon! Thus, naturally occurring carbon on Earth, therefore, is actually a mixture of isotopes, albeit a mixture that is 99% carbon-12. Isotope composition has proven to be a useful method for dating many rock layers and fossils.
Fig 2.8 Isotopes of Hydrogen. All hydrogen atoms have one proton and one electron. However, they can differ in the number of neutrons. (a) Most hydrogen atoms only contain one proton and one electron and no neutrons (b) A small amount of hydrogen exists as the isotope deuterium, which has one proton and one neutron in its nucleus, and (c) an even smaller amount contains one proton and two neutrons in its nucleus and is termed Tritium. Note that Tritium is unstable isotope and will breakdown over time. Thus, Tritium is a radioactive element.
Most elements exist as mixtures of isotopes. In fact, there are currently over 3,500 isotopes known for all the elements. When scientists discuss individual isotopes, they need an efficient way to specify the number of neutrons in any particular nucleus. A simple way of indicating the mass number of a particular isotope is to list it as a superscript on the left side of an element’s symbol. Atomic numbers are often listed as a subscript on the left side of an element’s symbol. Thus, we might see
which indicates a particular isotope of copper. The 29 is the atomic number, Z, (which is the same for all copper atoms), while the 63 is the atomic mass (A) of the isotope. To determine the number of neutrons in this isotope, we subtract 29 from 63: 63 − 29 = 34, so there are 34 neutrons in this atom.
The atomic masses indicated on the periodic table represents an average mass for each element based on the proportion of each isotope present on the Earth. This is why most of the atomic masses on the periodic table are not exact numbers. For example, the atomic mass of copper is 63.546 amu. This mass is an average of an element’s atomic masses, weighted by the natural abundance of each isotope. So how could we calculate atomic mass based on the natural abundance of different isotopes of an element?
Example: Calculating Atomic Mass Using Isotope Abundance
Extra Practice:
Try to work out the atomic mass for boron. Boron exists as a mixture that is 19.9% 10B and 80.1% 11B. Calculate the atomic mass. Check the periodic table for the correct answer!
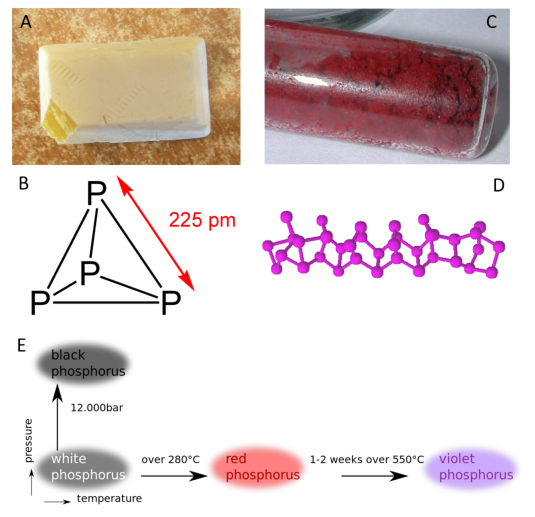
Allotropes of an element are different and separate from the term isotope and should not be confused. Some chemical elements can form more than one type of structural lattice, these different structural lattices are known as allotropes. This is the case for phosphorus as shown in Figure 2.9. White or yellow phosphorus forms when four phosphorus atoms align in a tetrahedral conformation (Fig 2.9). The other crystal lattices of phosphorus are more complex and can be formed by exposing phosphorus to different temperatures and pressures. For example, the cage-like lattice of red phosphorus can be formed by heating white phosphorus over 280oC (Fig 2.9). Note that allotropic changes affect how the atoms of the element interact with one another to form a 3-dimensional structure. They do not alter the sample with regard to the atomic isotope forms that are present, and DO NOT alter or affect the atomic mass (A) of the element.
Figure 2.9 Allotropes of Phosphorus. (A) White phosphorus exists as a (B) tetrahedral form of phosphorus, whereas (C) red phosphorus has a more (D) cage-like crystal lattice. (E) The different elemental forms of phosphorus can be created by treating samples of white phosphorus with increasing temperature and pressure.
Source: https://en.wikipedia.org/wiki/Allotropes_of_phosphorus
Different allotropes of different elements can have different physical and chemical properties and are thus, still important to consider. For example, oxygen has two different allotropes with the dominant allotrope being the diatomic form of oxygen, O2. However, oxygen can also exist as O3, ozone. In the lower atmosphere, ozone is produced as a by-product in automobile exhaust, and other industrial processes where it contributes to pollution. It has a very pungent smell and is a very powerful oxidant. It can cause damage to mucous membranes and respiratory tissues in animals. Exposure to ozone has been linked to premature death, asthma, bronchitis, heart attacks and other cardiopulmonary diseases. In the upper atmosphere, it is created by natural electrical discharges and exists at very low concentrations. The presence of ozone in the upper atmosphere is critically important as it intercepts very damaging ultraviolet radiation from the sun, preventing it from reaching the Earth’s surface. Thus, ozone can be a health hazard or a health protector, depending upon where it is found!
2.8 Electronic Structure of Atoms
Although we have discussed the general arrangement of subatomic particles in atoms, we have said little about how electrons occupy the space about the nucleus. Do they move around the nucleus at random, or do they exist in some ordered arrangement?
The modern theory of electron behavior is predicted by the field of quantum mechanics. The term quantum is defined as a discrete quantity or ‘packet’ of energy. For example, light has qualities of both a wave and a particle. Since it has properties of a particle, the energy of light is said to be quantized into discrete ‘packets’ of light particles called photons. Each photon of light, then carries a quantized amount of energy that is dependent on its frequency.
Electrons in atoms are also quantized and can exist at different energy levels depending on how far away from the nucleus of that atom that they are positioned. This is of interest, because the electrons are the mobile part of the atom and they are involved in forming chemical bonds. Understanding their positioning around the nucleus of the atom helps to predict how they will combine with other atoms to form chemical compounds. Electrons typically have higher energy, the farther away they are (on average) from the nucleus. However, the increasing energy of an electron does not proceed continuously like a ramp the farther away from the nucleus that it travels. Instead, the energy of an electron is quantized, meaning that the energy of an electron does not increase continuously, but instead increases by levels adding discrete packets of energy. This would be similar to walking up a staircase rather than a ramp. On a staircase, you can step up one step at a time, or maybe two steps at a time, but you can never step up a half of a step. Similarly, electrons travel between energy levels instantly, never having an energy amount in between two levels.
A total of four quantum numbers are used to describe completely the movement and trajectories of each electron within an atom. According to the Pauli Exclusion Principle, no two electrons can share the same combination of four quantum numbers. Thus, each electron in an atom has a unique set of quantum numbers that helps define the probable location of an electron within an atom. The quantum numbers that help to define electron location exist in a hierarchical order. This would be very similar to finding an address of a friend. If you don’t know your friend very well, you may only know the city where your friend lives. This doesn’t provide very much information. As you get to know them better, you may find out what neighborhood in the city that they live in. At a deeper level, you may find our what street they live on, and then at the deepest level, what their house number is on that street. However, knowing which house your friend lives in does not tell you where in the house you friend is at, maybe they are in the kitchen or the backyard. Determining the exact location of an electron is not possible. We can only find the approximate location or “address” of the electron.
The Four Electronic Quantum Numbers
There are a total of four quantum numbers: the principal quantum number (n), the orbital angular momentum quantum number (l), the magnetic quantum number (ml), and the electron spin quantum number (ms) that are used to describe the major characteristics and spatial distribution of electrons within an atom. The quantum numbers correspond to the following hierarchical layers: the principle quantum number (n) is the broadest classification and corresponds to the energy shell (this would be equivalent to the city in our address analogy), the orbital angular momentum quantum number (l) is the next layer and corresponds to the subshells (this would be the neighborhood in our address analogy), the magnetic quantum number (ml) corresponds to the electron orbitals (or the street where your friend lives), and electron spin quantum number (ms) defines the spins of electrons (or the house number in our address analogy).
n = shell
l = subshell
ml = orbital
ms = electron spin
The principal quantum number, n, designates the electron shell. Because n describes the most probable distance of the electrons from the nucleus, the larger the number n is, the farther the electron is from the nucleus and the larger the atom. The principal quantum number (n) can be any positive integer between 1 and 7. An n=1 designates the first principal shell (the innermost shell). The first principal shell is also called the ground state, or lowest energy state. When an electron is in an excited state or gains energy, it may jump to the second principle shell, where n=2. This process is called absorption because the electron is “absorbing” photons, or gaining energy. Thus, as the energy of the electron increases during absorption, so does the principal quantum number, e.g., if an electron in the n = 3 shell absorbs energy, it will jump to the fourth principal shell, n = 4. The opposite process is emission, where electrons “emit” or release energy as they fall from higher to lower principle shells. In this case, n decreases by whole numbers (packets or quanta of energy). Within atoms there is a maximum number of seven electron shells (n = 7), after which the atom becomes too unstable to hold electrons in place.
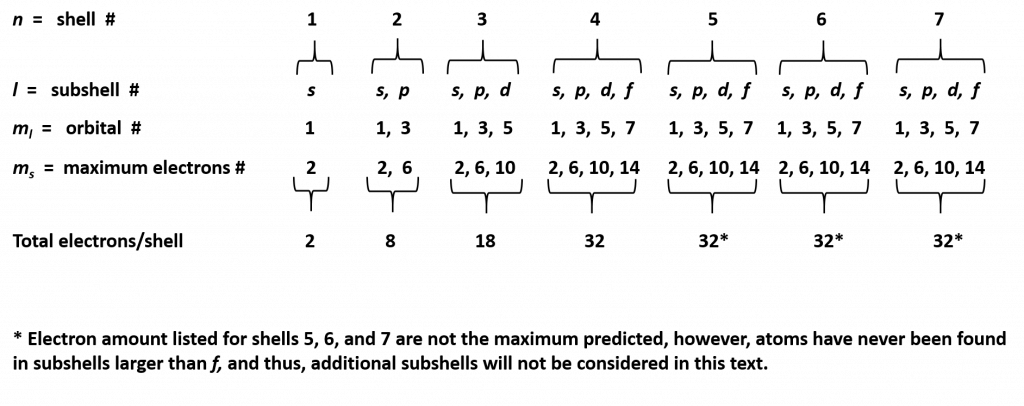
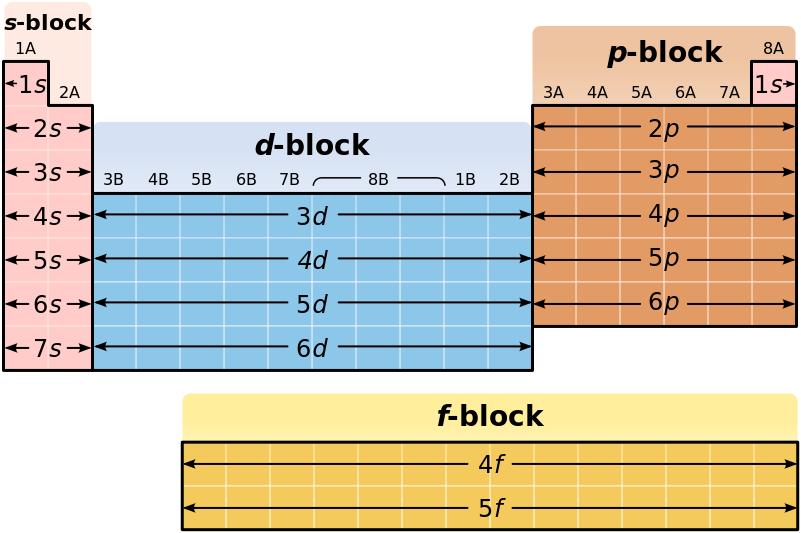
At a basic level, the energy shells can be thought of like the layering of an onion, with the first layer being the smallest and closest to the core of the nucleus, and the subsequent layers being larger and farther away from the core. Larger shells have more space and can hold more electrons. The general formula for determining how many electrons can be housed in each shell is 2n2 and is shown in Table 2.4. While this table predicts that that outer shells, which are the largest shells can contain 50, 72, and 98 electrons, elements that have this many electrons in those shells have never been discovered. It is likely that they are too big and unstable to exist.
Table 2.4 Maximum Number of Electrons Per Shell
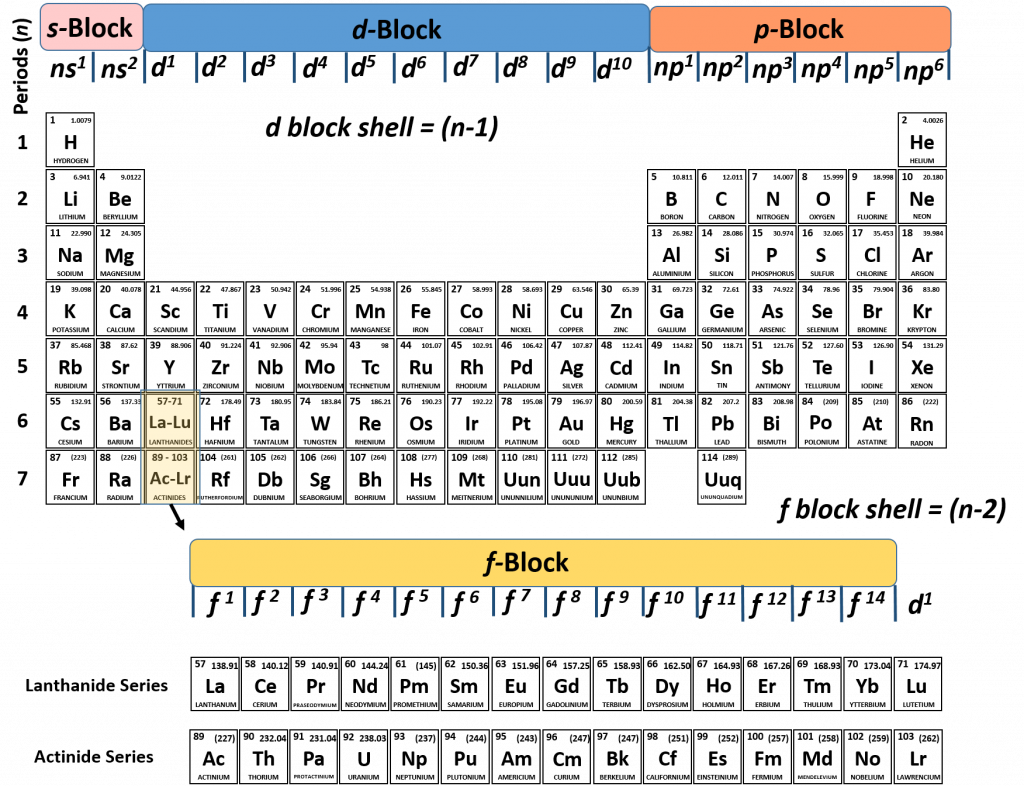
The periodic table allows us to easily determine how many protons (and therefore electrons) an element will have by showing the atomic number (Z) in each element box. Equally useful, the periodic table is set up to represent the different quantum numbers to facilitate the determination of electron configuration of an element. The principle quantum number (n) or number of shells present in an element are shown in the periods or rows of the periodic table (Figure 2.10). For example, if we look at the sodium atom, we will see that it is in row 3 of the periodic table. This means that it has three electron shells that can house electrons. As electrons fill their available orbital spaces, they always fill the shells starting at the lowest energy levels and going up to higher levels as needed. This rule can be formally noted as the Aufbau principle which states that electrons orbiting one or more atoms will fill the lowest available energy levels before filling higher energy levels.
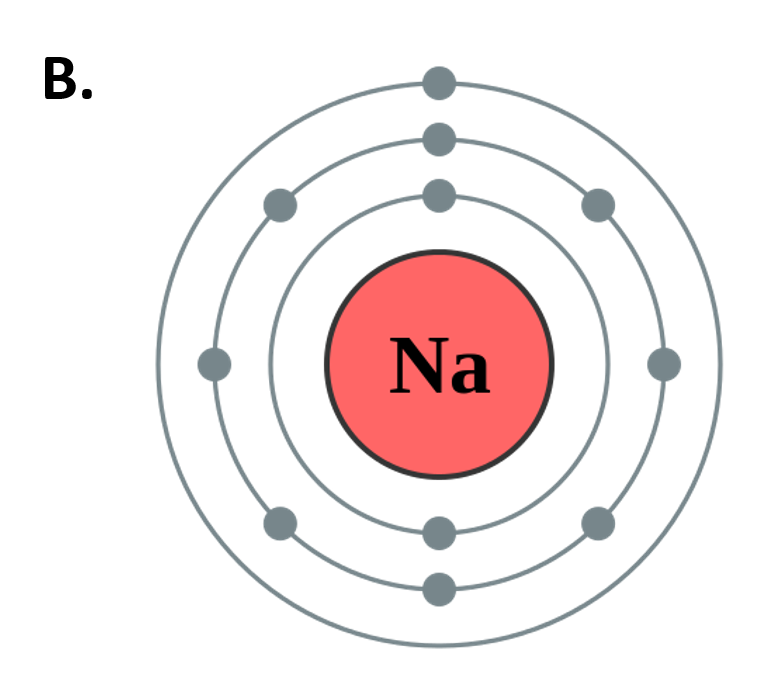
Figure 2.10 The Periods of the Periodic Table Represent Electron Shells (A) Each electron shell is represented by a row or period on the the periodic table. (B) A representation of the electron shells of the sodium atom. Sodium has an atomic number of 11, thus it has 11 protons and 11 electrons in the elemental form. The first and innermost electron shell can hold a total of 2 electrons, as indicated by the gray circles in the diagram. The second electron shell can hold 8 electrons and is completely full. The third electron shell has the capacity to hold 18 electrons, however, in sodium, there is only one more electron that needs to be placed after filling the first and second electron shells. Thus, the third electron shell of sodium only has 1 electron.
Figure 2.10B adapted from Pumbaa
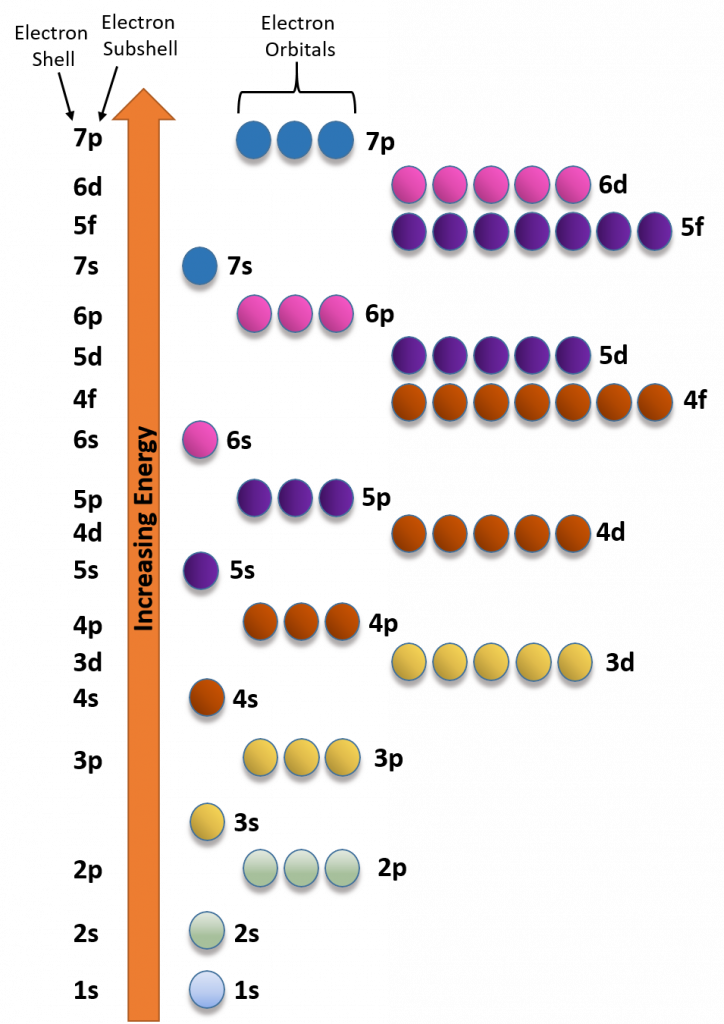
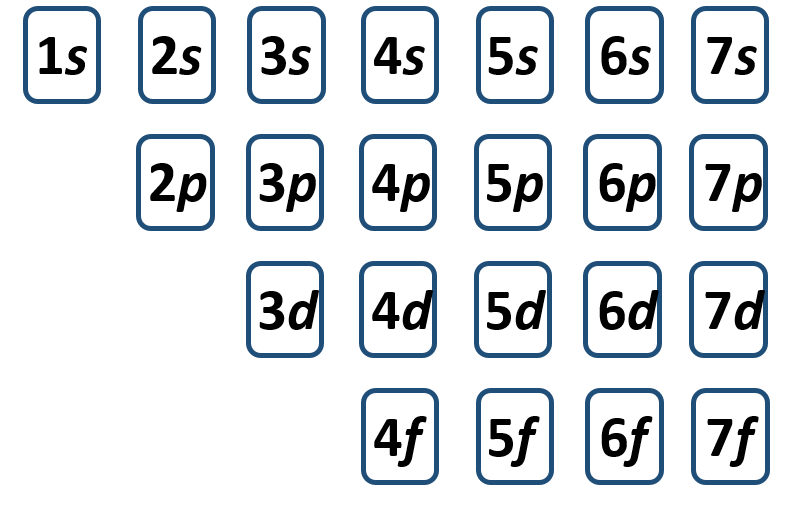
The electron shells are further subdivided into subshells that are represented by the second quantum number. There are four major types of subshells that are used to house electrons in known elements. These are termed the s, p, d, and f subshells. The first electron shell (n = 1) is so small that it only contains an s-subshell. The second electron shell (n = 2) is large enough to house an s- and a p-subshell. The third electron shell (n = 3) contains s-, p-, and d-subshells. The fourth shell and above (n = 4, 5, 6, and 7) contain all four electron subshells (s, p, d, and f). Shells 5-7 are predicted to have additional subshells, but elements using these subshells have never been discovered, so we will limit our discussion with the s, p, d, and f subshells.
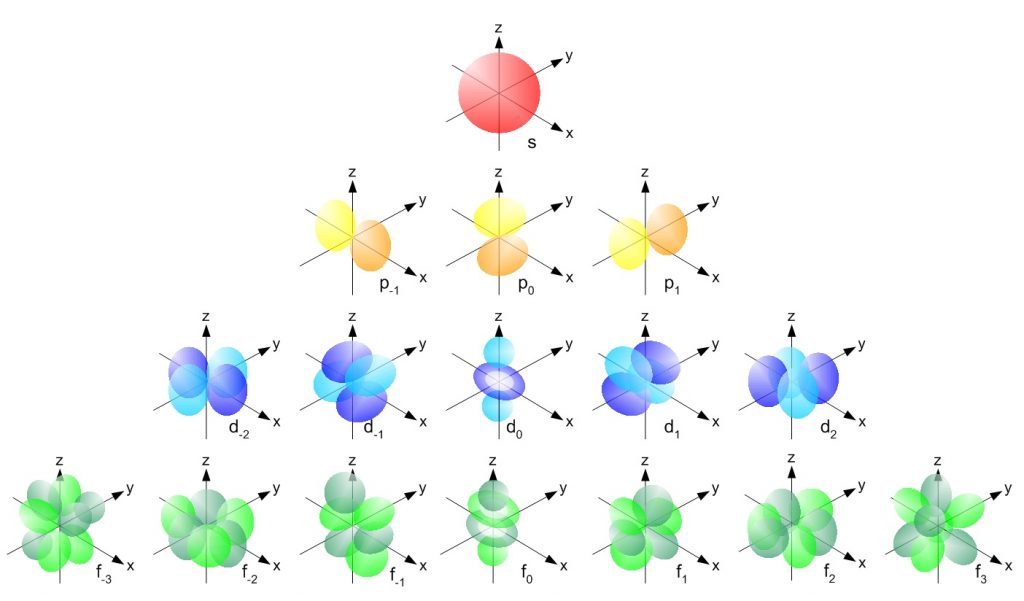
Each subshell, in turn, contains a specified number of electron orbitals arranged in unique shapes (Figure 2.11). Each orbital can then contain a total of 2 electrons rotating in opposite spin states. The s-subshell only contains 1 circular orbital that can house a total of two electrons. The p-subshell contains a total of 3 dumbbell-shaped orbitals that can house a total of 6 electrons. The d-subshell contains 5 uniquely shaped orbitals that can house a total of 10 electrons and the f-subshell contains 7 orbitals with a potential of housing 14 electrons. While the 5th – 7th shells are predicted to be able to house more electrons in even stranger g, h, and i subshells, there have never been any atoms discovered that contain enough electrons to utilize these locations. Atoms appear to become too large and unstable after the filling of the f-subshell orbitals in the 4th and 5th shell.
Figure 2.11 Orbital Shape Diagrams for the s, p, d, and f Subshells. A pair of electrons with opposite spin can be housed within each of the electron orbitals shown above.
We can summarize the availability of electron orbitals below:
Electron Orbital Filling Rules
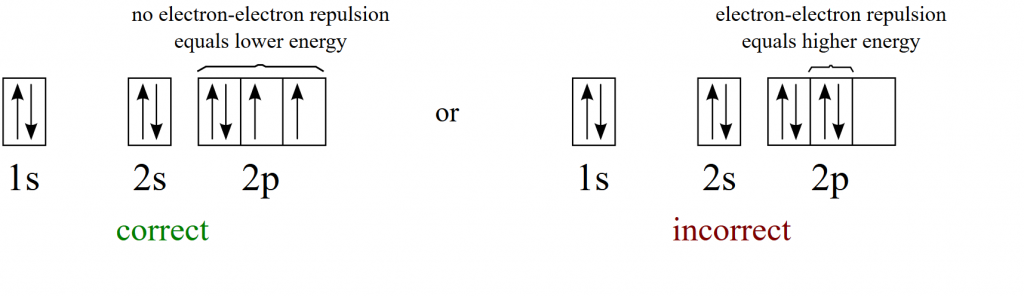
Now that we have defined the physical spaces that electrons can occupy, we need to determine the order of electron orbital filling. There are three major rules that we need to follow when filling electron orbitals. Recall that the Pauli Exclusion Principle excludes electrons from having the same quantum numbers, and thus, they cannot exist in the same place at the same time. Second according to the Aufbau principle, electrons orbiting one or more atoms will fill the lowest available energy levels before filling higher energy levels. Thus, the lowest energy levels must be filled with electrons before orbitals with higher energy can house electrons. The final rule that we need to follow is Hund’s rule which states that when electron orbitals have equal energy level, electrons must fill each of those orbitals as single electrons before they can begin to pair with electrons of opposite spin states. This is because electrons are negatively charged and naturally repel each other. Thus, they exist as far apart as possible. This is the most energetically stable way that electrons can fill orbitals.
Due to the strange shapes of the orbitals within the larger subshells, the energy levels of the orbitals don’t always correspond directly with their shell level. For example, the d-subshell orbitals have a higher energy than the s-subshell orbital from next shell level (i.e. the d-subshell orbitals from the 3rd shell have a higher energy and will fill with electrons later that the s-subshell from the 4th shell). Figure 2.12 depicts the energy levels from orbitals in the different subshells.
Figure 2.12 Electron Energy Filling Diagram. Orbitals with the lowest energy are filled with electrons before orbitals at higher energy levels.
Note that in the energy diagram above that there are many orbitals that share the same energy level. For example the three 2p orbitals have the same energy level. Thus, when these orbitals are filled with electrons, they are filled according to Hund’s Rule which states that single electrons will occupy orbitals at the same energy level before they will pair up. (If it helps, you can think to yourself…’electrons find each other repulsive and like to live alone’) The following example shows the correct and the incorrect way to fill the 2p orbitals.
Image provided by Wikimedia
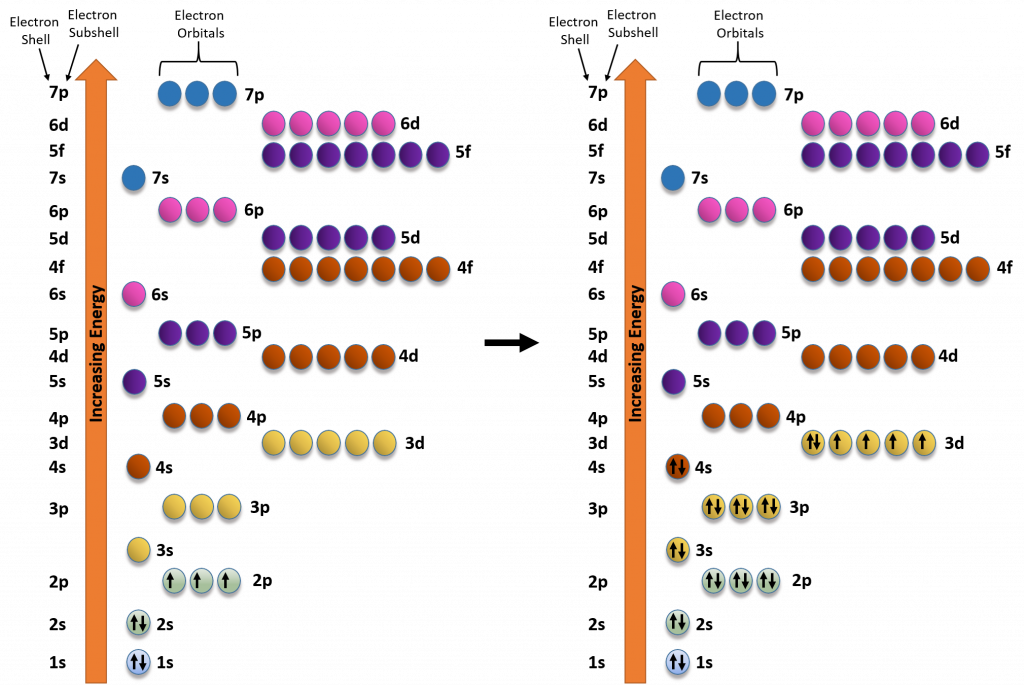
We can use the electron energy filling diagram to complete an example of how electrons in an element are arranged within the electron orbitals (Figure 2.13). Let’s take the example of Iron, (Fe). Iron has an atomic number of 26 or 26 protons. Thus in the elemental state, iron will also have 26 electrons. We will use arrows to represent our electrons within our diagram. Arrows pointing in opposite directions denote electrons that have opposite spin states. Note that the first set of electrons fills the 1s orbital. The next 8 electrons then fill the 2s and 2p orbitals. Note that when filling orbitals that have the same energy level, that the electrons have to follow Hund’s Rule, and fill these orbitals as single electrons first, and then pair up when there are no other options to exist in an orbital as a single electron. This filling pattern is noted in the lefthand diagram of the iron electron configuration. The lefthand diagram shows the active filling of the 2p orbitals with one electron at a time. After all three orbitals receive an electron, they will then pair up before filling the higher energy 3s orbital. Electron filling continues until all 26 electrons are placed. Note that in the case of iron, that the final electrons are placed in the 3d subshell orbitals following Hund’s Rule.
Figure 2.13 Electron Filling Diagram for the Element Iron (Fe). The lefthand diagram shows the partial filling of the electron orbitals during the assembly of an iron atom. Filling begins with the lowest energy orbital, which is the 1s obital. This is followed by the 2s orbital and the three 2p orbitals. Note that all of the 2p orbitals are at the same energy level. Thus, they are filled according to Hund’s Rule: each orbital at the same energy level will fill with one electron alone, until there are no other options. Then the electrons will pair to complete the filling of the 2p orbitals. The figure to the right denotes the completed electron filling diagram for the element iron. Note that the final electrons are placed in the 3d orbitals, and that they are placed to obey Hund’s Rule, leaving 4 of the 6 electrons at this energy level in the unpaired state.
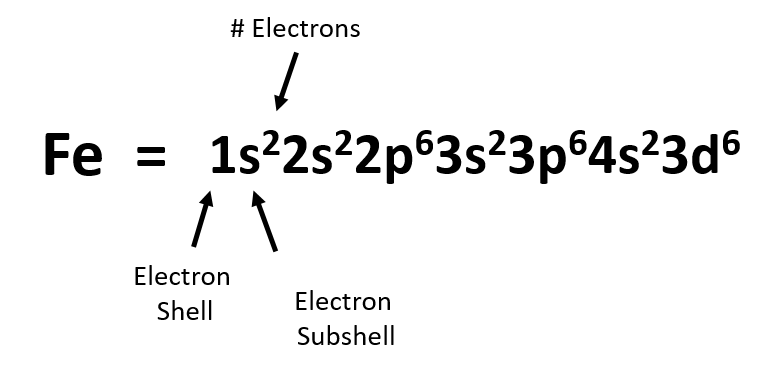
We can write the final electron configuration of iron (Fe) using a notation that denotes each electron shell and subshell and the superscript notation that refers the number of electrons present in the orbitals at that energy level. Remember that s-subshells can house 2 electrons, p-subshells can house 6 electrons, d-subshells can house 10 electrons, and f-subshells can house a maximum of 14 electrons.
From the diagram above, we can notice a few things. First, if we add up the superscript numbers, this should equal the total number of electrons in that atom. For example if we take the sum of the superscript numbers from the diagram above, we get:
2 + 2 + 6 +2 + 6 + 2 + 6 = 26
We can use this as a way to double check and make sure that we have constructed the electron configuration correctly.
The second piece of information that we can find very quickly is the number of electrons present in the outermost shell of the atom. The outermost shell of the atom is referred to as the valence shell, and it contains the most available and reactive electrons within the atom. The valence shell will always correspond to the highest shell number present in the atom that contains electrons. The other electron shells are known as inner electron shells. In the case of iron, the valence shell would be the 4th shell (or period on the periodic table). Shells 1-3 would then be the inner shells. Electrons housed in the valence shell are known as the valence electrons. Valence electrons are important because they are the ones that are most involved in chemical bonding, although sometimes electrons that are close to the valence electrons in energy, may also participate in bond formation. Most often these exceptions involve electrons in the d-subshell.
Note that due to the energy levels of the different subshells, that the only subshells that can exist in the valence shell are the s- and p-subshells. Both the d- and the f-subshells only fill after the s-orbital of the next higher shell level. Thus, they can never contribute to the number of valence electrons. Since the s-orbital can only house 2 electrons, and the p-orbitals can house 6 electrons, the maximum number of valence electrons possible for any atom is 8.
Concept Review
How many electrons are in the valence shell of Phosphorus? Phosphorus has an electron configuration of:
P = 1s22s22p63s23p3
Solution
In the analysis of the electron configuration of phosphorus, we can see that the 3rd shell is the valence shell. For phosphorus there are 2 electrons in the 3s orbital, and there are 3 electrons in the 3p orbitals. This is a total of 5 electrons in the outer shell or 5 valence electrons. Note that due to the energy levels of the different subshells, that the only subshells that can exist in the valence shell are the s- and p-subshells
Practice using the electron energy diagram to predict the electron configurations of the following atoms:
Boron, B
Carbon, C
Nitrogen, N
Oxygen, O
Fluorine, F
Neon, Ne
Solution:
B: 1s22s22p1
C: 1s22s22p2
N: 1s22s22p3
O: 1s22s22p4
F: 1s22s22p5
Ne: 1s22s22p6
Electron Configurations and the Periodic Table
It is not always convenient to use the energy filling diagram to predict the electron configuration of the elements. Therefore, to be able to predict electron configurations more easily, the periodic table has been arranged to represent the electron orbital filling patterns. This is what gives the periodic table its stair-step or jagged appearance. Once you know how to read the periodic table for electron configurations, it becomes very easy to write out the electron configuration of any element. Figure 2.14 shows a version of the periodic table that depicts the layout of the electron configurations.
Figure 2.14 The Periodic Table Corresponds to the Filling Patterns of the Electron Shells and Subshells.
This organization on the periodic table makes it easy to predict where an atom’s electron configuration ends and explains why elements within a family share so many similar characteristics! This is because they all share the same outer shell or valence shell electron configuration.
- Group 1A elements are the alkali metals and all have one electron in the outermost energy level because their electron configuration ends in s1.
- Group 2A elements are the alkaline earth metals and all have two electrons in the outermost energy level because their electron configuration ends in s2.
- All of the Transition Metals have two electrons in their outermost energy level because their highest shell electron configuration ends in s2.
- Group 3A elements have three electrons in the outermost energy level because their electron configuration ends in s2p1.
- Group 4A elements have four electrons in the outermost energy level because their electron configuration ends in s2p2.
- Group 5A elements all have five electrons in the outermost energy level because their electron configuration ends in s2p3.
- Group 6A elements all have six electrons in the outermost energy level because their electron configuration ends in s2p4.
- Group 7A elements are the halogens and all have seven electrons in the outermost energy level because their electron configuration ends in s2p5.
- Group 8A elements are the noble gases and all have eight electrons in the outermost energy level because their electron configuration ends in s2p6.
- Elements in group 8A have the most stable electron configuration in the outermost shell because the sub levels are completely filled with electrons.
Let’s do some practice problems using the following periodic table:
Figure 2.15 The Periodic Table and Electron Configurations. Note that each of the families on the periodic table corresponds to a specific electron configuration pattern. This makes it easy to determine where the electron configuration ends, and allows us to work backwards to complete the electron configuration.
Example 1
1. What is the electron configuration of Arsenic?
Solution:
1. We can use the periodic table like a map and determine where the final electron in Arsenic is placed:
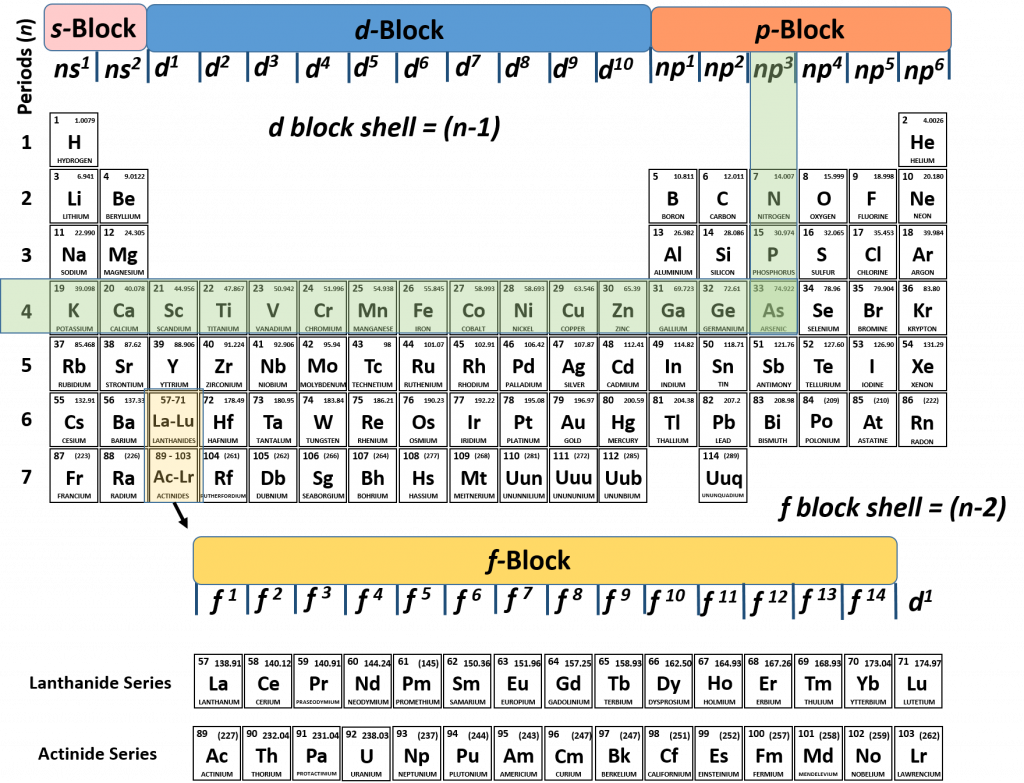
We can see that arsenic ends in the p-block at np3, and if we follow the period back to the left, we can see the n=4. Therefore, arsenic ends in 4p3. We know that according to Aufbau’s principle, that all of the lower energy subshells must be filled with electrons. We can then just walk backwards on the periodic table to read and fill in the lower energy subshells. If we walk backwards from arsenic along the previous periods of the periodic table, we run into the transition metals which represent the d-block. Remember that for the d-block subshell that the parent shell is (n-1). Since we are tracking back from arsenic in row 4, the d-block that we run into is n-1 or 4-1 = 3. So the next subshell would be 3d10, followed by 4s2, then 3p6, 3s2, 2p6, 2s2, and finally 1s2. Putting it all together, the electron configuration of arsenic is:
As = 1s22s22p63s23p64s23d104p3
Example 2
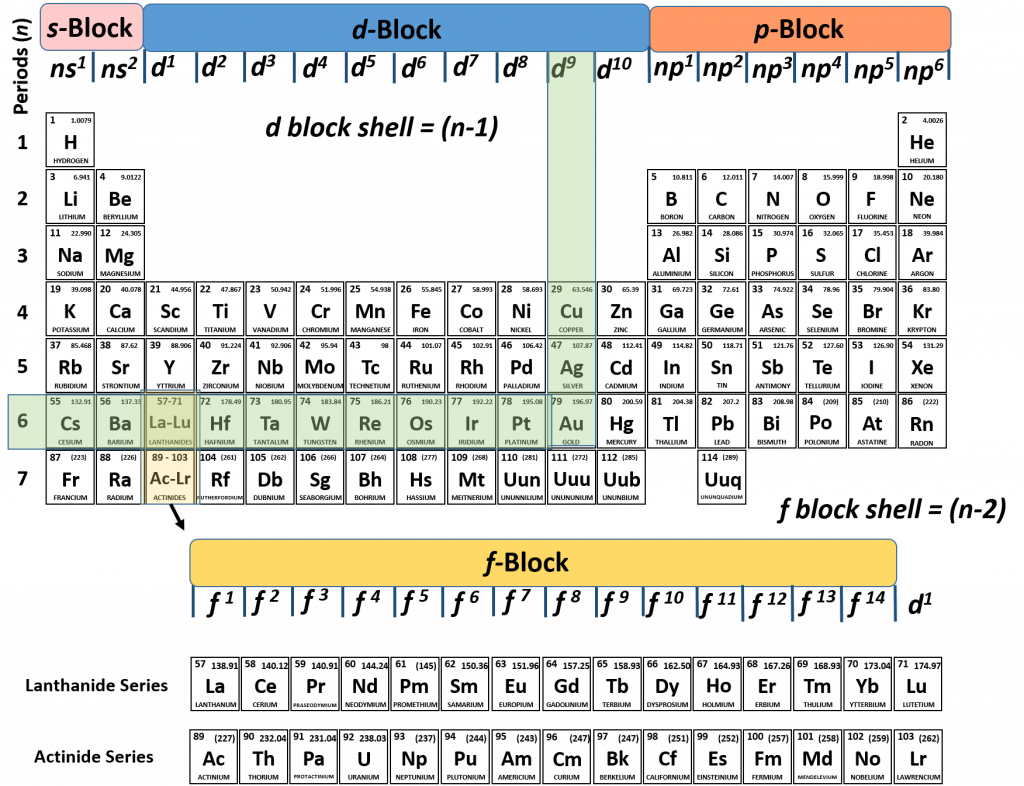
2. What stunning element ends with an electron configuration of 5d9? What is the complete electron configuration?
Solution
Again, we can use our knowledge of the periodic table to determine which element that this is represented by this configuration and help us write the full configuration.
The one thing that we have to be careful of when evaluating d-block elements, is that we remember that the d-block shell is always calculated as n-1. So for our problem, we know that our element in question end in 5d9. So the shell (n) or row that our element is in needs to be calculated using the formula n -1 = 5, which gives our final shell number of n = 6. Now we can simply follow the nd9 column down to the 6th row, and we find that Au or gold is our element.
To complete the electron configuration, we would simply walk back along the periodic table to fill in all of the lower energy subshells with electrons. So we start from gold at 5d9 and start walking back. What we notice is that the first thing we run into is an f-block (the lanthanide series). Note that the f-block shell is represented by (n-2). Since we are still in the 6th row, this would mean that the 6-2 = 4. The f-block is the 4f subshell. Recall that the f-subshell can hold a total of 14 electrons. Thus, the electron configuration is 4f14. This is followed by 6s2, 5p6, 4d10, 5s2, and so on, all the way back to 1s2. If we write out the full electron configuration of gold, it would be:
Au = 1s22s22p63s23p64s23d104p65s24d105p66s24f145d9
More Review Questions
- If an element is said to have an outermost electronic configuration of ns2np3, it is in what group in the periodic table?
- (a) Group 3A
- (b) Group 4A
- (c) Group 5A
- (d) Group 7A
- What is the general electronic configuration for the Group 8A elements? (Note: when we wish to indicate an electron configuration without specifying the exact energy level, we use the letter “n” to represent any energy level number. That is, ns2np3 represents any of the following; 2s22p3, 3s23p3, 4s24p3, and so on.)
- (a) ns2np6
- (b) ns2np5
- (c) ns2np1
- (d) ns2
- The group 2 elements are given what name?
- (a) alkali metals
- (b) alkaline earth metals
- (c) halogens
- (d) noble gases
- Using the diagram below, identify:
- (a) The alkali metal by giving the letter that indicates where the element would be located and write the outermost electronic configuration.
- (b) The alkaline earth metal by giving the letter that indicates where the element would be located and write the outermost electronic configuration.
- (c) The noble gas by giving the letter that indicates where the element would be located and write the outermost electronic configuration.
- (d) The halogen by giving the letter that indicates where the element would be located and write the outermost electronic configuration.
- (e) The element with an outermost electronic configuration of s2p3 by giving the letter that indicates where the element would be located.
- (f) The element with an outermost electronic configuration of s2p1 by giving the letter that indicates where the element would be located.

- In the periodic table, name the element whose outermost electronic configuration is found below. Where possible, give the name of the group.
- (a) 5s2
- (b) 4s23d104p1
- (c) 3s23p3
- (d) 5s24d105p2
- (e) 3s1
- (f) 1s2
- (g) 6s25d106p5
- (h) 4s24p4
Electron Configuration Solitaire
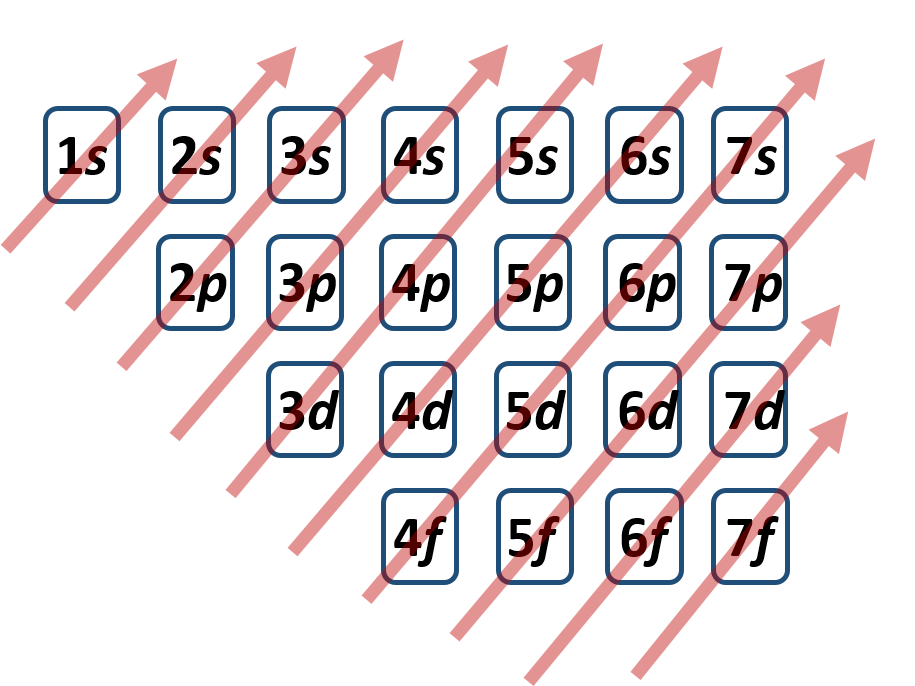
If you are having some trouble using the periodic table to determine electron configurations and don’t want to memorize the energy level diagram. There is one more way to help you determine the correct electron configuration of an element. This is also a good method to use to double check you work, when you are using a periodic table to help you determine electron configurations. The method is ‘electron configuration solitaire’. I call this method solitaire because that is what it reminds me of every time I draw this chart. Essentially, you are going to lay out all of the electron subshells into neat rows (left to right that are arranged by subshell type (s, p, d, and f). The first row will contain all of the s-subshells arranged from the lowest to the highest shell (n) number. So the first row would look like this:
Next align all of the other subshells (p, d and f) in neat rows directly under their appropriate shell lane. Once your diagram is complete, it will look like you have just dealt yourself a game of solitaire. In reality, you have just created a simple tool to enable you to write out any electron configuration.
To use your chart, you need to draw in diagonal arrows in the direction of electron filling. The final diagram tool should look like this:
It is read from left to right, starting at the bottom of each subsequent arrow.
Example
- What is the electronic configuration of Bromine?
Solution
For using the chart above, it is only necessary to determine how many electrons should be present in the element bromine. If we look back at the periodic table, we will see that there are 35 electrons. I find it also really quick to construct the electron configurations if I use a combination of the solitaire method and the periodic table method. I like to use the periodic table to find the end place of my electron configuration. If we look back again at bromine, we see that it is in the p-block, ending at 4p5. So we can follow the chart above, until we reach 4p5. If you don’t use the periodic table for this, you should keep track of your electrons and stop the configuration once you have placed all 35 electrons. Either method should give you the same result. Now just read off the appropriate shell/subshells and add in the appropriate amount of electrons for the superscripts:
Br = 1s22s22p63s23p64s23d104p5
Remember also, that adding up your electrons is a good quality check to make sure that the configuration matches the required number of electrons. In this case:
2 +2 + 6 + 2 + 6 + 2 + 10 + 5 = 35
Electron Configuration Shorthand
Writing out electron configurations can fast become tiresome, especially for larger elements like gold. Thus, chemists have made electron configuration shorthands for elements so that they wouldn’t have to keep rewriting all of the same subshell beginnings that make up most of the elements. This shorthand uses the Noble Gases as the shorthand reference point. Thus, when you are using the periodic table to determine an electron configuration, you only need to walk back on the periodic table until you run into your first Noble Gas. At that point the shorthand is written by placing the Nobel Gas in a hard bracket followed by the remaining electron configuration. Recall that the electron configuration that we constructed for gold (Au) was quite cumbersome and looked like:
Au = 1s22s22p63s23p64s23d104p65s24d105p66s24f145d9
With this electron configuration, if we use the periodic table to walk back, we run into our first noble gas at 5p6. (Hint: All the noble gases end at np6, so when you are walking back in you electron configurations, you should look for the first np6 that you see.) The noble gas at this position is Xenon (Xe). Thus, we can shorthand the Au configuration to look like:
Au = [Xe]6s24f145d9
Since xenon has all of the electrons up to 5p6, we can replace everything up to that point with the symbol for xenon. Essentially what we are then saying is that the electron configuration for gold looks like xenon + the 6s24f145d9
Learning the shorthand can save you a lot of time!
Extra Practice:
What are the shorthand electron configurations of:
Br = 1s22s22p63s23p64s23d104p5
and
As = 1s22s22p63s23p64s23d104p3
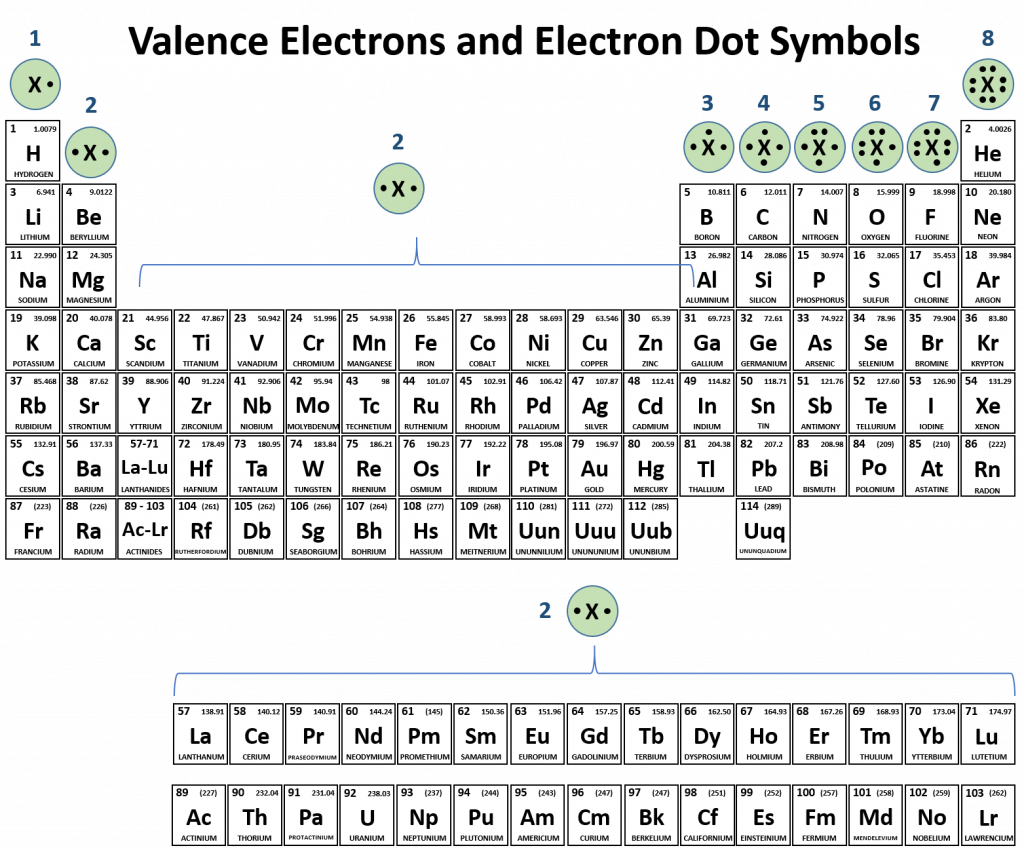
Electron-Dot Symbols
Although it is entirely possible to define the number of valence electrons in an atom through numbers, sometimes it is helpful to have a graphical representation. The graphical notation used for valence electrons is called an Electron-Dot Symbol. To draw an electron dot symbol, start with the abbreviation for the element of interest as the center, signifying the nucleus of the atom. From there, identify the number of valence electrons the atom has, and then add a single dot for each electron around the nucleus. Students often want to place these electron dots around the nucleus randomly, but it is useful for us to pair electron dots together as we might in an orbital. Following the same rules discussed above about orbital filling, the electron dot symbols for multiple atoms can be seen in the figure below. The easiest way to fill the orbitals is to start at one edge, add a dot, and fill in the rest of the dots one at a time by rotating clockwise on the edges of a square boxing in the nucleus until you have used all of the valence electrons. Note that each side should never have more than two dots, and that you should follow Hund’s rule when constructing your Electron-Dot Symbol. Each side should get one electron before the electrons are paired up.
Example
How many valence electrons does bromine have? draw the electron dot representation of bromine.
Solution
For the first part, we need to analyze the electron configuration of bromine and determine the valence shell and the electrons housed there:
We can see that the outer most shell is level 4, and that there are a total of 7 electrons housed there. Thus, bromine has 7 valence electrons. The electron dot symbol should look like:
Notice that this electron dot symbol for bromine looks just like the electron dot symbol for fluorine that is drawn above. This is because they are both in the halogen family. Recall that families share related properties because they have the same valence shell electron configuration. All of the halogens will have 7 electrons in their valence shell.
Since the periodic table is set up so that elements with similar electron configurations are aligned into family groups, it is also easy to use the periodic table to predict the valence electrons and draw the electron dot symbols for each of the family columns. This is shown in Figure 2.16.
Figure 2.16 Valence Electrons and Electron Dot Symbols.
2.9 Periodic Table Trends
Now that you have learned about the organization of the periodic table based on the electron configurations of the elements, we can continue to analyze the periodic table for trends that result from this organization.
Atomic Size
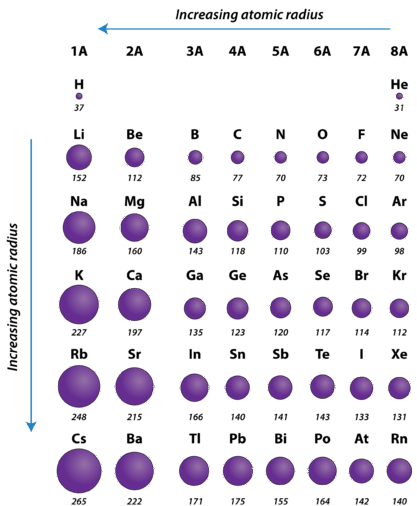
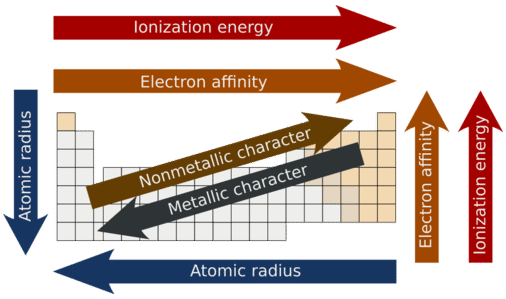
One important trend to be aware of is the way that atomic size changes as you move across a period or down a group in the periodic table. Atomic size is typically measured by the radius of the atom starting at the core of the nucleus, and reaching all the way out to the last valence electron. As you may predict, atomic size will increase as you move down a family group, due to the increased number of electron shells. This substantially increases the size of the electron cloud. What you may not so easily predict is that atomic size decreases as you go across a period. Although this may seem counter-intuitive, the decrease in size can be explained by thinking about the valence electron shell as you go across a period; we see that each element across a period has the same valence electron shell that it is filling with valence electrons. While the valence shell stays the same as you go across a period, the number of protons is increasing. Protons, being positively charged, have a pull on the negatively charged electrons out in the electron cloud. As the number of protons and electrons increases across a period, they have an attractive pull on one another. This results in a tightening of the electron cloud and a reduction in the atomic nuclei. In other words, because the outermost electron shell remains the same across a period, that shell gets pulled progressively closer and closer to the nucleus of the atom as you go across a period. So the overall periodic trend for atomic radius (size) is that atoms get smaller as you go across a period, and they get larger as you go down a family group (Figure 2.17).
Figure 2.17 Atomic Radii of Select Elements Across the Periodic Table
Overall:
- Atomic radius is determined as half the distance between the nuclei of two identical atoms bonded together.
- The atomic radius of atoms generally decreases from left to right across a period.
- The atomic radius of atoms generally increases from top to bottom within a group.
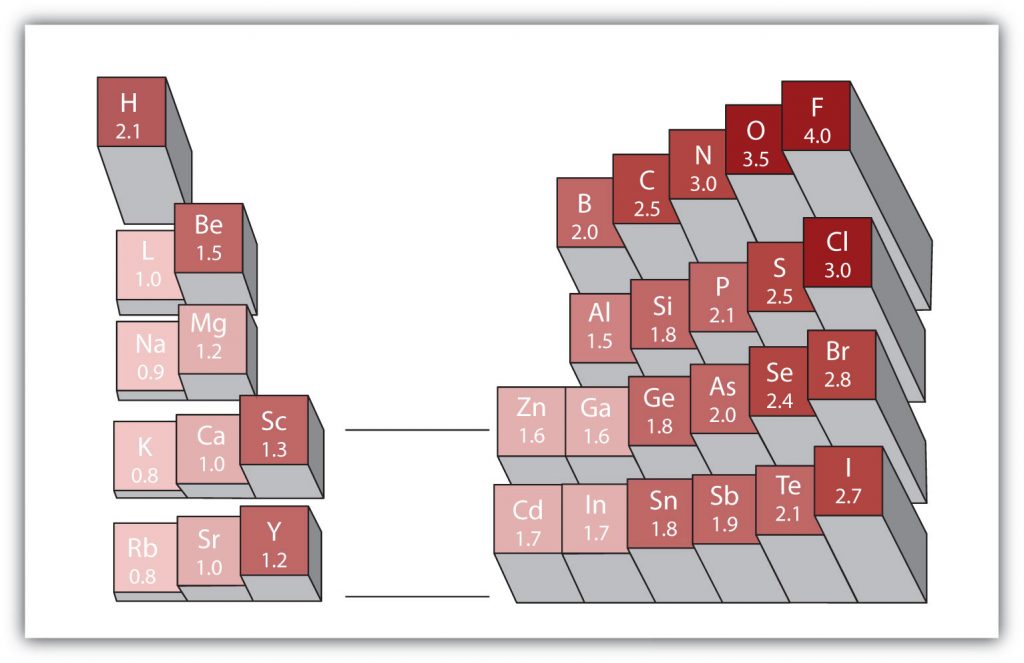
Electronegativity
Another important periodic trend to be aware of is how electronegativity differences can be identified. Electronegativity is the measure of an atom’s tendency to attract a bonding pair of electrons. There are various numerical scales for rating electronegativity. Figure 4.3 shows one of the most popular—the Pauling scale. The Pauling scale assigns fluorine, the most electronegative atom, a 4.0 while less electronegative atoms have smaller grades. We will see in chapters 3 and 4 that electronegativity plays an important role in chemical bonding. The trends for electronegativity in the periodic table are that electronegativity increases as you go across a period, and increases as you go up a group, with fluorine being the most electronegative atom. Noble gases are given an electronegativity rating of 0 due to their inherent stability, which keeps them from forming bonds with other atoms.
Figure 2.18 Electronegativities of Various Elements. The Pauling Scale for electronegativities has the value for fluorine atoms set at 4.0, the highest value.
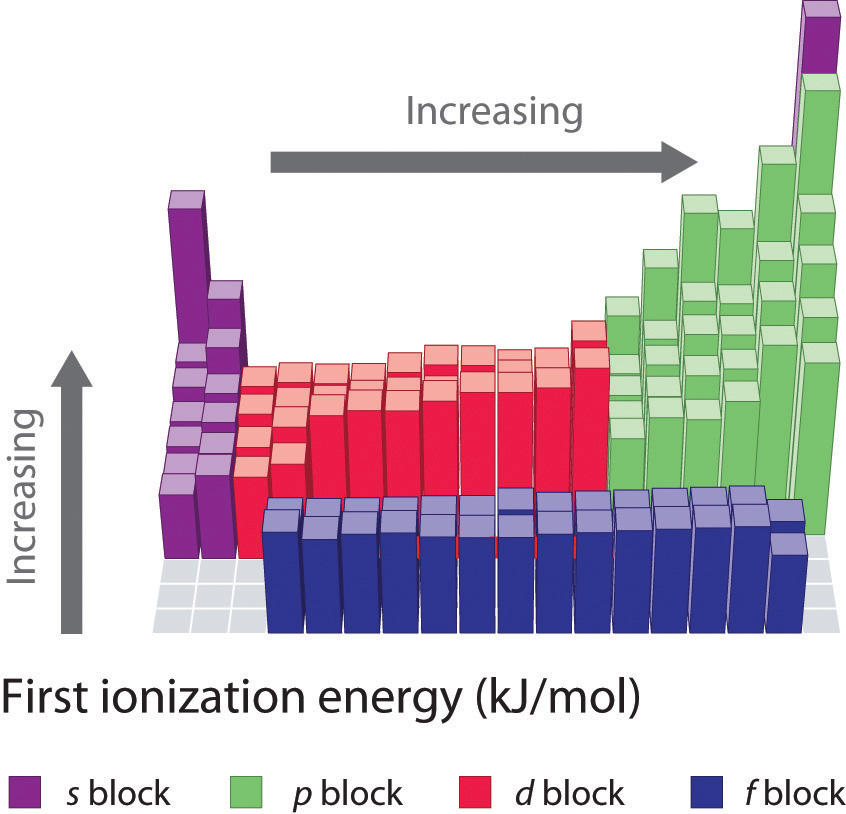
Ionization Energy
Another periodic trend that you will be expected to know is the trend for ionization energy. Ionization energy is defined as the amount of energy required to remove the most loosely bound electron of an atom. How tightly bound the electrons of an atom are will affect the amount of energy required to remove one of the valence electrons. Electrons that are closer to the nucleus are going to be more tightly held than those that are further away and will require more energy to pull them off of the atom. For this reason, we see that ionization energy decreases as you go down a family group and the atoms get larger. This same concept can be applied to atoms across a period. We will see that the highest ionization energy will be found on the right side of the period where the atoms are the smallest, and the lowest ionization energy on the left where the atoms have a larger radii. In general, ionization energy decreases as you go down a family group, and increases as you go across a period from left to right (Figure 2.19).
Figure 2.19 First Ionization Energies for the Elements of the Periodic Table.
Metallic and Nonmetallic Character
Metallic character refers to the level of reactivity of a metal. Metals tend to lose electrons in chemical reactions, as indicated by their low ionization energies. Within a compound, metal atoms have relatively low attraction for electrons, as indicated by their low electronegativities. By following the trend summary in the figure below, you can see that the most reactive metals would reside in the lower left portion of the periodic table. The most reactive metal is cesium, which is not found in nature as a free element. It reacts explosively with water and will ignite spontaneously in air. Francium is below cesium in the alkali metal group, but is so rare that most of its properties have never been observed.
The metallic character increases as you go down a group. Since the ionization energy decreases going down a group (or increases going up a group), the increased ability for metals lower in a group to lose electrons makes them more reactive. In addition, the atomic radius increases going down a group, placing the outer electrons further away from the nucleus and making that electron less attracted by the nucleus.
Nonmetals tend to gain electrons in chemical reactions and have a high attraction for electrons within a compound. These tendencies are known as nonmetallic character. The most reactive nonmetals reside in the upper right portion of the periodic table. Since the noble gases are a special group because of their lack of reactivity, the element fluorine is the most reactive nonmetal. It is not found in nature as a free element. Fluorine gas reacts explosively with many other elements and compounds and is considered to be one of the most dangerous known substances.
Note that there is no clear division between metallic and nonmetallic character. As we move across the periodic table, there is an increasing tendency to accept electrons (nonmetallic) and a decrease in the possibility that an atom would give up one or more electrons.
Overall
- Metallic character refers to the level of reactivity of a metal to donate electrons during a chemical reaction.
- Nonmetallic character relates to the tendency of an element to accept electrons during chemical reactions.
- Metallic character increases going down a family group and decreases going across a period.
- Nonmetallic character increases going from left to right across the periodic table and decreases going down a family group.
The following figure summarizes all of the major periodic trends within the periodic table
Figure 2.20 Summary of Major Periodic Trends
2.10 Focus on the Environment – Nuclear Energy
Introduction to Radioactivity
In section 2.7 you learned about elemental isotopes and that atoms are defined by the number of protons held within the nucleus. Atomic theory in the nineteenth century presumed that nuclei had fixed compositions. But in 1896, the French scientist Henri Becquerel found that a uranium compound placed near a photographic plate made an image on the plate, even if the compound was wrapped in black cloth. He reasoned that the uranium compound was emitting some kind of radiation that passed through the cloth to expose the photographic plate. Further investigations showed that the radiation was a combination of particles and electromagnetic rays, with its ultimate source being the atomic nucleus. These emanations were ultimately called, collectively, radioactivity.
There are three main forms of radioactive emissions. The first is called an alpha particle, which is symbolized by the Greek letter α. An alpha particle is composed of two protons and two neutrons and is the same as a helium nucleus. (We often use 24He to represent an alpha particle.) It has a 2+ charge. When a radioactive atom emits an alpha particle, the original atom’s atomic number decreases by two (because of the loss of two protons), and its mass number decreases by four (because of the loss of four nuclear particles). We can represent the emission of an alpha particle with a chemical equation—for example, the alpha-particle emission of uranium-235 is as follows:
92235U → 24He+90231Th
Rather than calling this equation a chemical equation, we call it a nuclear equation to emphasize that the change occurs in an atomic nucleus. How do we know that a product of this reaction is90231Th? We use the law of conservation of matter, which says that matter cannot be created or destroyed. This means we must have the same number of protons and neutrons on both sides of the nuclear equation. If our uranium nucleus loses 2 protons, there are 90 protons remaining, identifying the element as thorium. Moreover, if we lose four nuclear particles of the original 235, there are 231 remaining. Thus we use subtraction to identify the isotope of the Th atom—in this case, 90231Th.
Chemists often use the names parent isotope and daughter isotope to represent the original atom and the product other than the alpha particle. In the previous example, 92235U
is the parent isotope, and 90231Th is the daughter isotope. When one element changes into another in this manner, it undergoes radioactive decay.
The second major type of radioactive emission is called a beta particle, symbolized by the Greek letter β. A beta particle is an electron ejected from the nucleus (not from the shells of electrons about the nucleus) and has a 1− charge. We can also represent a beta particle as -10e. The net effect of beta particle emission on a nucleus is that a neutron is converted to a proton. The overall mass number stays the same, but because the number of protons increases by one, the atomic number goes up by one. Carbon-14 decays by emitting a beta particle:
614C → 714N +-10e
Again, the sum of the atomic numbers is the same on both sides of the equation, as is the sum of the mass numbers. (Note that the electron is assigned an “atomic number” of –1, equal to its charge.)
The third major type of radioactive emission is not a particle but rather a very energetic form of electromagnetic radiation called gamma rays, symbolized by the Greek letter γ. Gamma rays themselves do not carry an overall electrical charge, but they may knock electrons out of atoms in a sample of matter and make it electrically charged (for which gamma rays are termed ionizing radiation). For example, in the radioactive decay of radon-222, both alpha and gamma radiation are emitted, with the latter having an energy of 8.2 × 10−14 J per nucleus decayed:
86222Rn → 24He + 84218Po + γ
This may not seem like much energy, but if 1 mol of Rn atoms were to decay, the gamma ray energy would be 4.9 × 107 kJ! That is enough energy to power an average American home for an entire year.
Table 2.5 Characteristics of Radioactive Particles
Nuclear Fission Reactions and Energy
Occasionally, an atomic nucleus breaks apart into smaller pieces in a radioactive process called spontaneous fission. Typically, the daughter isotopes produced by fission are a varied mix of products, rather than a specific isotope as with alpha and beta particle emission. Often, fission produces excess neutrons that will sometimes be captured by other nuclei, possibly inducing additional radioactive events. Uranium-235 undergoes spontaneous fission to a small extent. One typical reaction is
92235U → 56139Ba + 3694Kr + 2 01n
where 01n is a neutron. As with any nuclear process, the sums of the atomic numbers and mass numbers must be the same on both sides of the equation. Spontaneous fission is found only in large nuclei. The smallest nucleus that exhibits spontaneous fission is lead-208. Fission is the radioactive process used in nuclear power plants and one type of nuclear bomb.
When a critical mass of a fissile isotope is achieved, the resulting flux of neutrons can lead to a self-sustaining reaction. Natural uranium is a mixture of isotopes, and includes a small proportion (0.720%) of the fissile isotope, U-235. When the nucleus of a U-235 atom is split by a neutron, it discharges two or three additional neutrons and releases energy in the form of heat (Fig 2.21). The additional neutrons released can react with other U-235 particles and form a sustaining chain reaction. To sustain such a reaction, a critical amount (3-5%) of U-235 is required in the source material. Thus, naturally occurring uranium cannot be used for nuclear fission. The uranium must first be enriched for the U-235 isotope through a complicated and difficult process. Compared to energy grade uranium which is enriched to 3-5% of U-235, bomb grade uranium is highly enriched (>90% U-235).
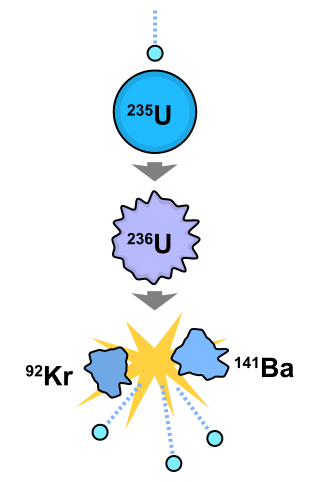 Figure 2.21 Nuclear Fission Reaction of U-235. The addition of a neutron to U-235 results in the formation of an unstable U-236 atom that splits into Kr-92 and Ba-141 and releases 3 neutrons. This figure was created by Fastfission
Figure 2.21 Nuclear Fission Reaction of U-235. The addition of a neutron to U-235 results in the formation of an unstable U-236 atom that splits into Kr-92 and Ba-141 and releases 3 neutrons. This figure was created by Fastfission
A variety of techniques can be used to control the flow of neutrons from such a reaction, which allows nuclear fission reactions to be maintained at safe levels. With regards to energy production, if the neutron flow in a reactor is carefully regulated so that only enough heat is released to boil water, then the resulting steam can be used to produce electricity. Thus a nuclear reactor is similar in many respects to the conventional power plants, which burn coal or natural gas to generate electricity; the only difference is the source of the heat that converts water to steam. Many levels of control are required, along with a fail-safe design, because otherwise the chain reaction can accelerate so rapidly that it releases enough heat to melt or vaporize the fuel and the container, a situation that can release enough radiation to contaminate the surrounding area. Light-water reactors are the most common type of fission reactor, and are used extensively to produce electricity in countries such as Japan, Israel, South Korea, Taiwan, and France—countries that lack large reserves of fossil fuels. The essential components of a light-water reactor are depicted in Figure 2.22. Approximately 11% of the world’s energy is generated by nuclear power, with more than a dozen countries obtaining more than 30% of their energy from nuclear sources.
Figure 2.22 A Light-Water Nuclear Fission Reactor for the Production of Electric Power. The fuel rods are made of a corrosion-resistant alloy that encases the partially enriched uranium fuel; controlled fission of 235U in the fuel produces heat. Water surrounds the fuel rods and moderates the kinetic energy of the neutrons, slowing them to increase the probability that they will induce fission. Control rods that contain elements such as boron, cadmium, or hafnium, which are very effective at absorbing neutrons, are used to control the rate of the fission reaction. A heat exchanger is used to boil water in a secondary cooling system, creating steam to drive the turbine and produce electricity. The large hyperbolic cooling tower, which is the most visible portion of the facility, condenses the steam in the secondary cooling circuit; it is often located at some distance from the actual reactor.
All existing nuclear power plants have similar components, although different designs use different fuels and operating conditions. Fuel rods containing a fissile isotope in a structurally stabilized form (such as uranium oxide pellets encased in a corrosion-resistant zirconium alloy) are suspended in a cooling bath that transfers the heat generated by the fission reaction to a secondary cooling system. The heat is used to generate steam for the production of electricity. In addition, control rods are used to absorb neutrons and thereby control the rate of the nuclear chain reaction. Control rods are made of a substance that efficiently absorbs neutrons, such as boron, cadmium, or, in nuclear submarines, hafnium. Pulling the control rods out increases the neutron flux, allowing the reactor to generate more heat, whereas inserting the rods completely stops the reaction, a process called “scramming the reactor.”
All nuclear reactors require a powerful cooling system to absorb the heat generated in the reactor core and create steam that is used to drive a turbine that generates electricity. In 1979, an accident occurred when the main water pumps used for cooling at the nuclear power plant at Three Mile Island in Pennsylvania stopped running, which prevented the steam generators from removing heat. Eventually, the zirconium casing of the fuel rods ruptured, resulting in a meltdown of about half of the reactor core. Although there was no loss of life and only a small release of radioactivity, the accident produced sweeping changes in nuclear power plant operations. The US Nuclear Regulatory Commission tightened its oversight to improve safety.
The main disadvantage of nuclear fission reactors is that the spent fuel, which contains too little of the fissile isotope for power generation, is much more radioactive than the unused fuel due to the presence of many daughter nuclei with shorter half-lives than 235U. The decay of these daughter isotopes generates so much heat that the spent fuel rods must be stored in water for as long as 5 yr before they can be handled. Even then, the radiation levels are so high that the rods must be stored for many, many more years to allow the daughter isotopes to decay to nonhazardous levels. How to store these spent fuel rods for hundreds of years is a pressing issue that has not yet been successfully resolved. As a result, some people are convinced that nuclear power is not a viable option for providing our future energy needs, although a number of other countries continue to rely on nuclear reactors for a large fraction of their energy.
Uncontrolled nuclear fission reactions are relatively rare, but they have occurred at least 18 times in the past. One of the most recent occurred on April 25–26, 1986, at the Chernobyl nuclear power plant in the former Union of Soviet Socialist Republics (USSR; now in the Ukraine). During testing of the reactor’s turbine generator, a series of mechanical and operational failures caused a chain reaction that quickly went out of control, destroying the reactor core and igniting a fire that destroyed much of the facility and released a large amount of radioactivity. Thirty people were killed immediately, and the high levels of radiation in a 20 mile radius forced nearly 350,000 people to be resettled or evacuated. In addition, the accident caused a disruption to the Soviet economy that is estimated to have cost almost $13 billion. It is somewhat surprising, however, that the long-term health effects on the 600,000 people affected by the accident appear to be much less severe than originally anticipated. Initially, it was predicted that the accident would result in tens of thousands of premature deaths, but an exhaustive study almost 20 yr after the event suggests that 4000 people will die prematurely from radiation exposure due to the accident. Although significant, in fact it represents only about a 3% increase in the cancer rate among the 600,000 people most affected, of whom about a quarter would be expected to eventually die of cancer even if the accident had not occurred.
The most recent event resulted from the damaged Fukushima Dai-ichi plant after the March 11, 2011, earthquake and tsunami that devastated Japan. The plant used fresh water for cooling nuclear fuel rods to maintain controlled, sustainable nuclear fission. When the water supply was disrupted, so much heat was generated that a partial meltdown occurred. Radioactive iodine levels in contaminated seawater from the plant were over 4300 times the regulated safety limit. To put this in perspective, drinking one liter of fresh water with this level of contamination is the equivalent to receiving double the annual dose of radiation that is typical for a person. Dismantling the plant and decontaminating the site is estimated to require 30 years at a cost of approximately $12 billion.
Suggested Assignment:
Watch the Frontline Episode: Nuclear Aftershocks (Found here: https://www.pbs.org/video/frontline-nuclear-aftershocks/) Following the video, write a 500 word essay about whether or not you feel that nuclear energy should be used in the United States at the Indian Point Nuclear Power Plant. Be sure to include pros and cons within your argument.
2.11 Chapter Summary
Dalton’s Atomic Theory proposed that matter is made up of tiny particles called atoms that cannot be broken into smaller pieces. During a chemical reaction, atoms are rearranged, but they do not break apart, nor are they created or destroyed. An element is a substance that cannot be broken down into simpler chemical substances. There are about 90 naturally occurring elements known on Earth. The smallest unit of an element is the atom. All atoms of the same element are identical in mass and other properties, whereas atoms of different elements differ in mass and other properties.
The elements can be divided into three major classes: The metals, metalloids, and nonmetals. Metals are typically shiny, very dense, have high melting points, and are good conductors. Nonmetals are generally brittle, dull, have low melting points, and they are generally poor conductors. Metalloids have properties of both metals and nonmetals.
Dmitri Mendeleev organized the elements into a chart based on their similar characteristics and properties. Today this chart is known as the periodic table of the elements. Within the periodic table group, or family of elements, is a vertical column of the periodic table. Elements are placed into families due to their similar properties, characteristics, and reactivities. Group 1 elements are known as the alkali metals and are the most reactive elements of the metal class. Alkaline earth metals are found in group 2 and are almost as reactive as the group 1 metals. The transition metals are the larger block of elements extending from Groups 3-12 (also known as the group B elements). Transition metals have high melting points and boiling points, often form colored compounds that are highly stable, and they can serve as good catalysts. A catalyst is an agent that helps to speed up a chemical reaction without itself being changed in the process. Group 17 elements, known as halogens, contains very reactive nonmetals that often exist as diatomic elements (F2, Cl2, Br2, I2). Group 18 elements, the noble gases are extremely stable, unreactive, and rarely form compounds.
Atoms are made up of extremely small subatomic particles called protons, neutrons, and electrons. Protons (positively charged particles), and neutrons (electrically neutral particles) form the core or nucleus of an atom. Electrons are extremely small, negatively charged particles that form an electron cloud, which orbits the nucleus. The atomic number (Z) refers the the number of protons present in an element and is the defining feature of an element. The atomic mass (A) of an element is the sum of the protons and neutrons within that element.
Atoms of the same element (have the same atomic number) that have different numbers of neutrons are called isotopes. Most elements exist as isotopes. In fact, over 3,500 isotopes are known for the different elements. The atomic mass reported on the periodic table is the relative mass of the different isotopes of an element based on their abundance on the Earth. Some chemical elements can also form more than one type of structural lattice, these different structural lattices are known as allotropes. Allotropic changes affect how the atoms of the element interact with one another to form a 3-dimensional structure, but do not alter the sample with regard to the atomic isotope forms that are present, and do not alter or affect the atomic mass (A) of the element.
Understanding the electron configuration within an element is important for understanding the reactivity of the element. The modern theory of electron behavior is predicted by the field of quantum mechanics. The term quantum is defined as a discrete quantity or ‘packet’ of energy. Electrons in atoms can exist at different energy levels depending on how far away from the nucleus of that atom that they are positioned. Electrons typically have higher energy, the farther away they are (on average) from the nucleus. Four quantum numbers (n, l, ml, and ms) are used to assign the position of an electron within at atom. The principle quantum number (n) refers to the electron shells and corresponds to each period or row on the periodic table. The orbital angular momentum quantum number (l) refers to the electron subshell classification which can be of the s, p, d, or f categories. The magnetic quantum number (ml) refers to the electron orbitals, and the electronic spin number (ms) refers to the electron spin state of the electrons. Each orbital can house 2 electrons, each of which have an opposite spin. Each subshell can house a specific number of electron orbitals: s-subshells have one orbital and can house a total of 2 electrons, p-subshells have three obitals and can house a total of 6 electrons, d-subshells have five orbitals and can house a total of 10 electrons, and f-subshells have seven orbitals and can house a total of 14 electrons.
Electron orbitals are filled according to three major rules. The Pauli Exclusion Principle states that electrons cannot occupy the same space at the same time, and thus, no two electrons can share the same combination of four quantum numbers. Second according to the Aufbau principle, electrons orbiting one or more atoms will fill the lowest available energy levels before filling higher energy levels. The final rule that we need to follow is Hund’s rule which states that when electron orbitals have equal energy level, electrons must fill each of those orbitals as single electrons before they can begin to pair with electrons of opposite spin states. The periodic table and the electron configuration solitaire tool can be used to determine the electron configuration of any element. Electron configurations can be written using the noble gas shorthand rules.
The valence shell of an element is the outermost electron shell. The electrons housed within the valence shell are the most reactive electrons in an atom and are essential for forming chemical bonds with other elements. There are a total of eight electrons that can be housed in the valence shell of any atom. The periodic table can be used to predict the number of valence electrons present within an atom and electron dot symbols provide a graphic representation of the valence shell electrons.
Due to the organization of the periodic table according to proton and electron configurations, a number of interesting elemental trends can be observed. Atomic size, as measured by the atomic radius of an atom, increases and you move down a family group, and decreases as you move from left to right down a period or a row on the periodic table. The Electronegativity of an atom is the measure of an atom’s tendency to attract a bonding pair of electrons, and can be thought of as electron affinity. Electronegativity increases as you go from left to right across the periods of the periodic table and it tends to decrease as you move down family groups. Ionization energy is defined as the amount of energy required to remove the most loosely bound electron of an atom. Ionization energy tends to increase as you move across the periods of the periodic table from left to right, and decreases as you move down a family group. Metallic character refers to the level of reactivity of a metal, whereas nonmetallic character refers to the level of reactivity of nonmetals. The metallic character of the elements tends to go up as you move down a family group of elements and goes down as you move from left to right across a row of the periodic table. Concomitantly, nonmetallic character tends to go down as you move down a family group of elements and goes up as you move from the left to the right across the periodic table.
Video Tutorial of Electron Configurations and Ionization Energy By: Paul Anderson and Bozeman Science
Homework Chapter 2
Part 1: Atomic Structure
2.12 References
Chapter 2 materials have been adapted and modified from the following creative commons resources unless otherwise noted:
1. Anonymous. (2012) Introduction to Chemistry: General, Organic, and Biological (V1.0). Published under Creative Commons by-nc-sa 3.0. Available at: http://2012books.lardbucket.org/books/introduction-to-chemistry-general-organic-and-biological/index.html
2. Poulsen, T. (2010) Introduction to Chemistry. Published under Creative Commons by-nc-sa 3.0. Available at: http://openedgroup.org/books/Chemistry.pdf
3. OpenStax (2015) Atoms, Isotopes, Ions, and Molecules: The Building Blocks. OpenStax CNX.Available at: http://cnx.org/contents/be8818d0-2dba-4bf3-859a-737c25fb2c99@12.
4. LibreTexts (2017) Chem 121: Chapter 2 Atomic Structure. https://chem.libretexts.org/LibreTexts/Valley_City_State_University/Chem_121/Chapter_2%3A_Atomic_Structure/2.03%3A_Families_and_Periods_of_the_Periodic_Table
5. Robson, G.(2006) Wikipedia. https://en.wikipedia.org/wiki/Electron_shell
6. LibreTexts (2016) Physical and Theoretical Chemistry. https://chem.libretexts.org/Core/Physical_and_Theoretical_Chemistry/Quantum_Mechanics/09._The_Hydrogen_Atom/Atomic_Theory/Electrons_in_Atoms/Electronic_Orbitals
7. High School Chemistry/Families on the Periodic Table. (2016) Wikibooks. https://en.wikibooks.org/wiki/High_School_Chemistry/Families_on_the_Periodic_Table#Alkali_Metals_Have_One_Electron_in_Their_Outer_Energy_Level
8. Anonymous. (2012) Principles of General Chemistry (V1.0). Published under Creative Commons by-nc-sa 3.0. Available at: http://webmis.highland.cc.il.us/~jsullivan/principles-of-general-chemistry-v1.0/index.html
9. Key, Jessie A. and Ball, D.W. (2011) Introductory Chemistry – 1st Canadian Edition. Published as an Open Source Textbook under Creative Commons by-nc-sa 4.0. Available at: https://opentextbc.ca/introductorychemistry/chapter/radioactivity-2/
10. World Nuclear Association. (2016) Uranium and Depleted Uranium. Published as part of the information library. Available at: http://www.world-nuclear.org/information-library/nuclear-fuel-cycle/uranium-resources/uranium-and-depleted-uranium.aspx
11. Anonymous (2012) Applied Nuclear Chemistry Chapter from Principles of General Chemistry (V.1.0) Published as an Open Source Textbook under Creative Commons by-nc-sa 3.0. Available at: http://webmis.highland.cc.il.us/~jsullivan/principles-of-general-chemistry-v1.0/s24-05-applied-nuclear-chemistry.html