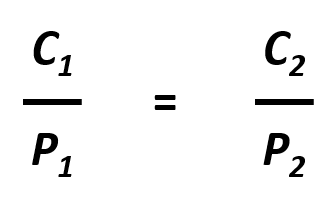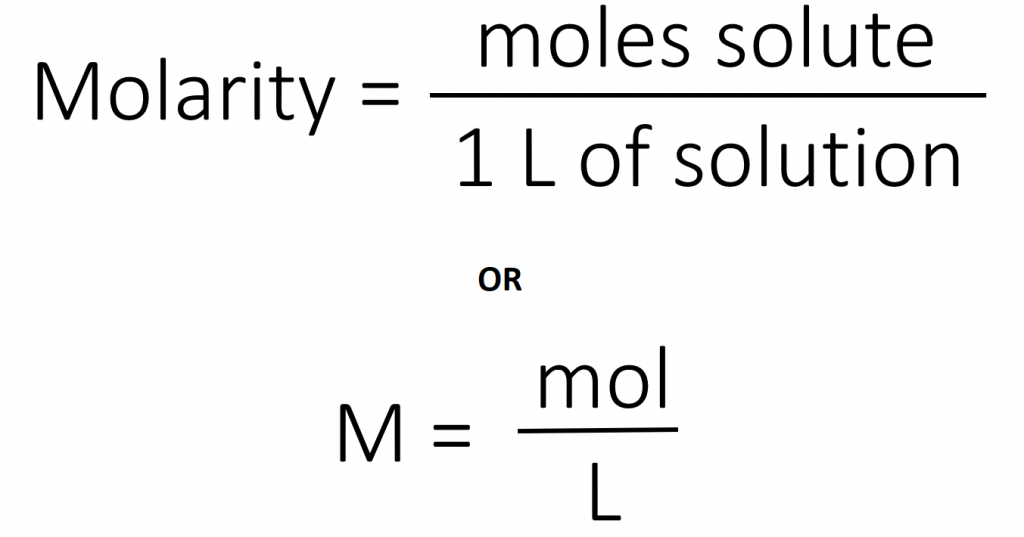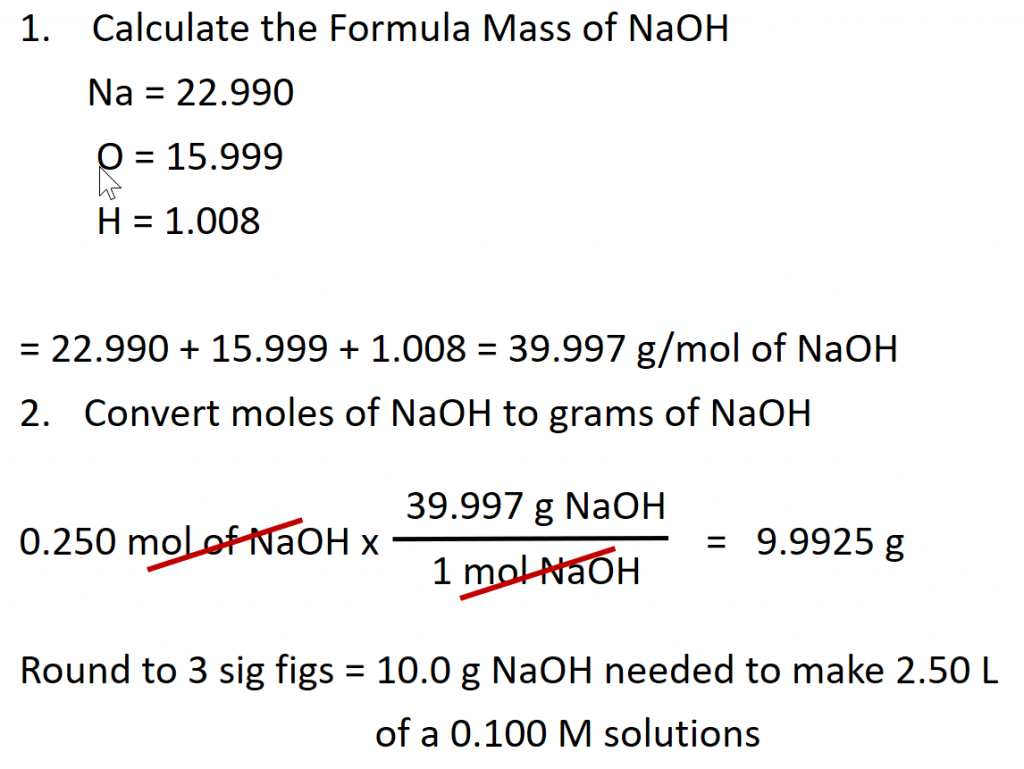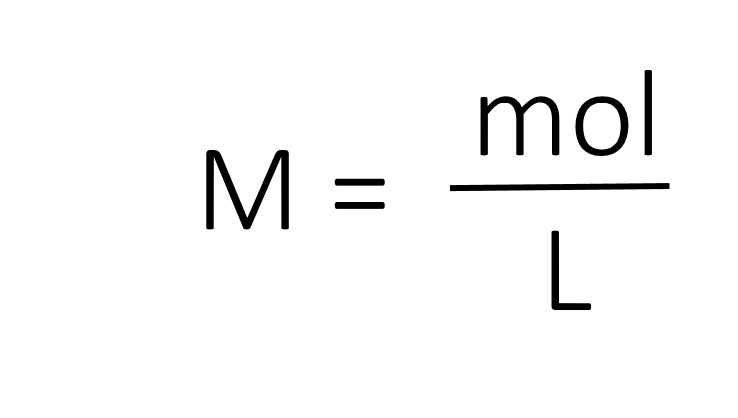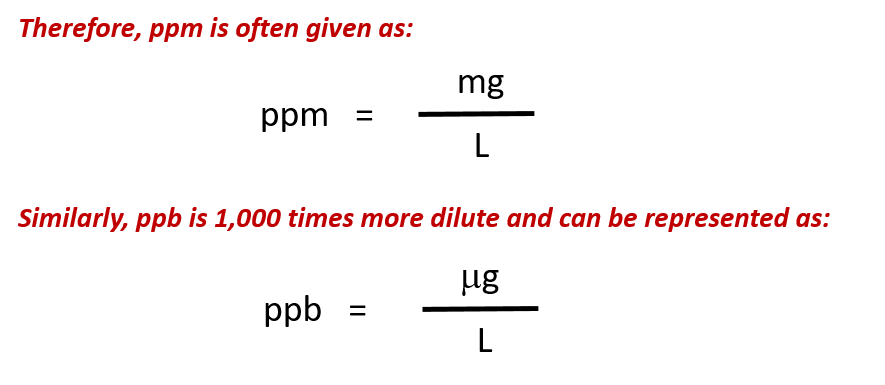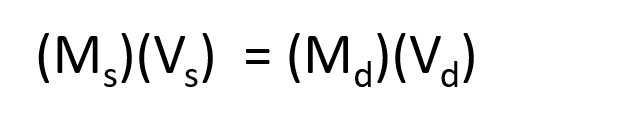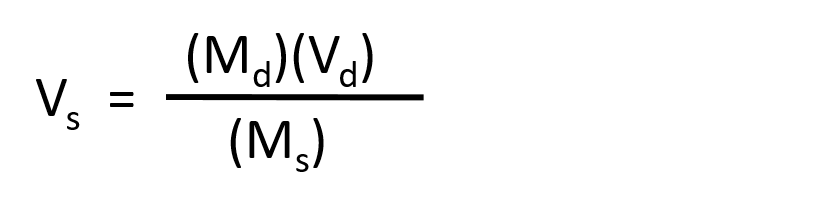Home » Student Resources » Online Chemistry Textbooks » CH150: Preparatory Chemistry » CH150: Chapter 7 – Solutions
MenuCH150: Preparatory Chemistry
Chapter 7: Solutions And Solution Stoichiometry
7.1 Introduction
7.2 Types of Solutions
7.3 Solubility
7.4 Temperature and Solubility
7.5 Effects of Pressure on the Solubility of Gases: Henry’s Law
7.6 Solid Hydrates
7.7 Solution Concentration
7.7.1 Molarity
7.7.2 Parts Per Solutions
7.8 Dilutions
7.9 Ion Concentrations in Solution
7.10 Summary
7.11 References
7.1 Introduction:
Recall from Chapter 1 that solutions are defined as homogeneous mixtures that are mixed so thoroughly that neither component can be observed independently of the other. Solutions are all around us. Air, for example, is a solution. If you live near a lake, a river, or an ocean, that body of water is not pure H2O but most probably a solution. Much of what we drink—for example, soda, coffee, tea, and milk are solutions. Solutions are a large part of everyday life. A lot of the chemistry occurring around us happens in solution. In fact, much of the chemistry that occurs in our own bodies takes place in solution, and many solutions—such as the Ringer’s lactate IV solution—are important in healthcare. In our understanding of chemistry, we need to understand a little bit about solutions. In this chapter, you will learn about the special characteristics of solutions, how solutions are characterized, and some of their properties.
Skills to Develop
- Define these terms: solution, solute, and solvent.
- Distinguish solutions, mixtures, and colloids.
- Describe various types of solutions.
- Distinguish unsaturated, saturated, and supersaturated solutions.
The major component of the solution is called solvent, and the minor component(s) are called solute. If both components in a solution are 50%, the term solute can be assigned to either component. When a gaseous or solid material dissolves in a liquid, the gas or solid material is called the solute. When two liquids dissolve in each other, the major component is called the solvent and the minor component is called the solute.
Many chemical reactions are carried out in solutions, and solutions are also closely related to our everyday lives. The air we breathe, the liquids we drink, and the fluids in our body are all solutions. Furthermore, we are surrounded by solutions such as the air and waters (in rivers, lakes and oceans).
On the topic of solutions, we include the following sections.
- Types of Solutions: gaseous, liquid and solid solutions are based on the states of the solution.
- Solution Stoichiometry: expressing concentration in various units (mass per unit volume, moles per unit volume, percentage and fractions), reaction stoichiometry calculations involving solutions.
- Solutions of Electrolytes: solutions of acids, bases, and salts in which the solutes dissociate into positive and negative hydrated ions.
- Metathesis or Exchange Reactions: reaction of electrolytes leading to neutral molecules, gases, and solids.
Solving problems of solution stoichiometry requires the concepts introduced in stoichiometry in Chapter 6, which also provides the basis for the discussion on reactions.
(Back to the Top)
7.2 Types of Solutions
In Chapter 1, you were introduced to the concept of a mixture, which is a substance that is composed of two or more substances. Recall that mixtures can be of two types: Homogeneous and Heterogeneous, where homogeneous mixtures combine so intimately that they are observed as a single substance, even though they are not. Heterogeneous mixtures, on the other hand, are non-uniform and have regions of the mixture that look different from other regions of the mixture. Homogeneous mixtures can be further broken down into two classifications: Colloids and Solutions. A colloid is a mixture that contains particles with diameters ranging from 2 to 500 nm. Colloids appear uniform in nature and have the same composition throughout but are cloudy or opaque. Milk is a good example of a colloid. True solutions have particle sizes of a typical ion or small molecule (~0.1 to 2 nm in diameter) and are transparent, although they may be colored. This chapter will focus on the characteristics of true solutions.
Material exists in three states: solid, liquid, and gas. Solutions also exist in all these states:
- Gaseous mixtures are usually homogeneous and are commonly gas-gas solutions. For quantitative treatment of this type of solutions, we will devote a unit to gases. The atmosphere is a gaseous solution that consists of nitrogen, oxygen, argon, carbon dioxide, water, methane, and some other minor components. Some of these components, such as water, oxygen, and carbon dioxide may vary in concentration in different locations on the Earth depending on factors such as temperature and altitude.
- When molecules of gas, solid or liquid are dispersed and mixed with those of liquid, the homogeneous (uniform) states are called liquid solutions. Solids, liquids and gases dissolve in a liquid solvent to form liquid solutions. In this chapter, most of the chemistry that we will discuss occurs in liquid solutions where water is the solvent.
- Many alloys, ceramics, and polymer blends are solid solutions. Within a certain range, copper and zinc dissolve in each other and harden to give solid solutions called brass. Silver, gold, and copper form many different alloys with unique colors and appearances. Alloys and other solid solutions are important in the world of materials chemistry.
(Back to the Top)
7.3 Solubility
The maximum amount of a substance that can be dissolved in a given volume of solvent is called solubility. Often, the solubility in water is expressed in gram/100 mL. A solution that has not reached its maximum solubility is called an unsaturated solution. This means that more solute could still be added to the solvent and dissolving would still occur.
A solution that has reached the maximum solubility is called a saturated solution. If more solute is added at this point, it will not dissolve into the solution. Instead it will remain precipitated as a solid at the bottom of the solution. Thus, one can often tell that a solution is saturated if extra solute is present (this can exist as another phase, such as gas, liquid, or solid). In a saturated solution there is no net change in the amount of solute dissolved, but the system is by no means static. In fact, the solute is constantly being dissolved and deposited at an equal rate. Such a phenomenon is called equilibrium. For example:
In special circumstances, a solution may be supersaturated. Supersaturated solutions are solutions that have dissolved solute beyond the normal saturation point. Usually a condition such as increased temperature or pressure is required to create a supersaturated solution. For example, sodium acetate has a very high solubility at 270 K. When cooled, such a solution stays dissolved in what is called a meta-stable state. However, when a seeding crystal is added to the solution, the extra solute will rapidly solidify. During the crystallization process, heat is evolved, and the solution becomes warm. Common hand warmers use this chemical process to generate heat.
Video showing the crystallization of a supersaturated solution of sodium acetate. Video by : North Carolina School of Science and Mathematics
So how can we predict the solubility of a substance?
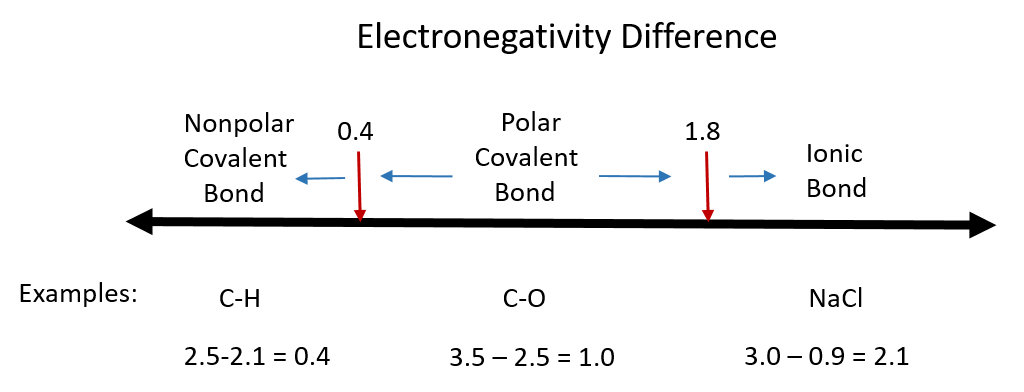
One useful classification of materials is polarity. As you read about covalent and ionic compounds in Chapters 3 and 4, you learned that ionic compounds have the highest polarity forming full cations and anions within each molecule as electrons are donated from one atom to another. You also learned that covalent bonds could be polar or nonpolar in nature depending on whether or not the atoms involved in the bond share the electrons unequally or equally, respectively. Recall that the electronegativity difference can be used to determine the polarity of a substance. Typically an ionic bond has an electronegativity difference of 1.8 or above, whereas a polar covalent bond is between 0.4 to 1.8, and a nonpolar covalent bond is 0.4 or below.
Figure 7.1 Electronegativity Difference Diagram. The diagram above is a guide for discerning what type of bond forms between two different atoms. By taking the difference between the electronegativity values for each of the atoms involved in the bond, the bond type and polarity can be predicted. Note that full ionic character is rarely reached, however when metals and nonmetals form bonds, they are named using the rules for ionic bonding.
Substances with zero or low electronegativity difference such as H2, O2, N2, CH4, CCl4 are nonpolar compounds, whereas H2O, NH3, CH3OH, NO, CO, HCl, H2S, PH3 higher electronegativity difference are polar compounds. Typically compounds that have similar polarity are soluble in one another. This can be described by the rule:
Like Dissolves Like.
This means that substances must have similar intermolecular forces to form solutions. When a soluble solute is introduced into a solvent, the particles of solute can interact with the particles of solvent. In the case of a solid or liquid solute, the interactions between the solute particles and the solvent particles are so strong that the individual solute particles separate from each other and, surrounded by solvent molecules, enter the solution. (Gaseous solutes already have their constituent particles separated, but the concept of being surrounded by solvent particles still applies.) This process is called solvation and is illustrated in Figure 7.2. When the solvent is water, the word hydration, rather than solvation, is used.
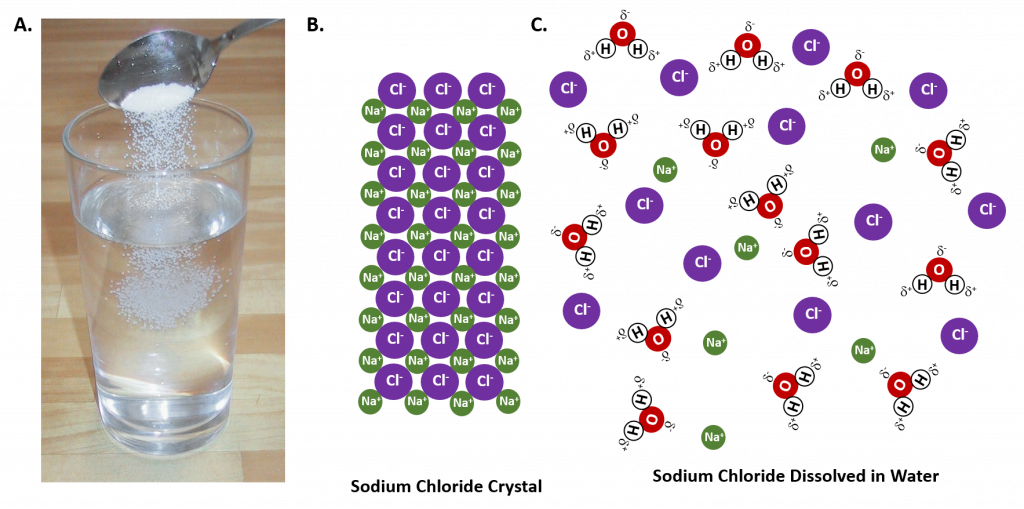
In general polar solvents dissolve polar solutes whereas nonpolar solvents will dissolve nonpolar solutes. Overall, the solution process depends on the strength of the attraction between the solute particles and the solvent particles. For example, water is a highly polar solvent that is capable of dissolving many ionic salts. Figure 7.2 shows the solution process, where water act as the solvent to dissolve the crystalline salt, sodium chloride (NaCl). Note that when ionic compounds dissolve in a solvent they break apart into free floating ions in solution. This enables the compound to interact with the solvent. In the case of water dissolving sodium chloride, the sodium ion is attracted to the partial negative charge of the oxygen atom in the water molecule, whereas the chloride ion is attracted to the partial positive hydrogen atoms.
Figure 7.2: The Process of Dissolving. When an ionic salt, such as sodium chloride, shown in (A), comes into contact with water, the water molecules dissociate the ion molecules of the sodium chloride into their ionic state, shown as a molecular model in (B) the solid crystalline lattice of sodium chloride, and (C) the sodium chloride dissolved in the water solvent. (Photo of sodium chloride provided by Chris 73 ).
Many ionic compounds are soluble in water, however, not all ionic compounds are soluble. Ionic compounds that are soluble in water exist in their ionic state within the solution. You will notice in Figure 7.2 that the sodium chloride breaks apart into the sodium ion and the chloride ion as it dissolves and interacts with the water molecules. For ionic compounds that are not soluble in water, the ions are so strongly attracted to one another that they cannot be broken apart by the partial charges of the water molecules. The following table can be used to help you predict which ionic compounds will be soluble in water.
Table 7.1 Solubility Rules
The dissociation of soluble ionic compounds gives solutions of these compounds an interesting property: they conduct electricity. Because of this property, soluble ionic compounds are referred to as electrolytes. Many ionic compounds dissociate completely and are therefore called strong electrolytes. Sodium chloride is an example of a strong electrolyte. Some compounds dissolve but dissociate only partially, and solutions of such solutes may conduct electricity only weakly. These solutes are called weak electrolytes. Acetic acid (CH3COOH), the compound in vinegar, is a weak electrolyte. Solutes that dissolve into individual neutral molecules without dissociation do not impart additional electrical conductivity to their solutions and are called nonelectrolytes. Polar covalent compounds, such as table sugar (C12H22O11), are good examples of nonelectrolytes.
The term electrolyte is used in medicine to mean any of the important ions that are dissolved in aqueous solution in the body. Important physiological electrolytes include Na+, K+, Ca2+, Mg2+, and Cl−. Sports drinks such as Gatoraid have combinations of these key electrolytes, to help replenish electrolyte loss following a hard workout.
Similarly, solutions can also be made by mixing two compatible liquids together. The liquid in the lower concentration is termed the solute, and the one in higher concentration the solvent. For example, grain alcohol (CH3CH2OH) is a polar covalent molecule that can mix with water. When two similar solutions are placed together and are able to mix into a solution, they are said to be miscible. Liquids that do not share similar characteristics and cannot mix together, on the other hand, are termed immiscible. For example, the oils found in olive oil, such as oleic acid (C18H34O2) have mainly nonpolar covalent bonds which do not have intermolecular forces that are strong enough to break the hydrogen bonding between the water molecules. Thus, water and oil do not mix and are said to be immiscible.
Other factor such as temperature and pressure also affects the solubility of a solvent. Thus, in specifying solubility, one should also be aware of these other factors.
(Back to the Top)
7.4 Temperature and Solubility
When considering the solubility solids, the relationship of temperature and solubility is not simple or predictable. Figure 7.3 shows plots of the solubilities of several organic and inorganic compounds in water as a function of temperature. Although the solubility of a solid generally increases with increasing temperature, there is no simple relationship between the structure of a substance and the temperature dependence of its solubility. Many compounds (such as glucose and CH3CO2Na) exhibit a dramatic increase in solubility with increasing temperature. Others (such as NaCl and K2SO4) exhibit little variation, and still others (such as Li2SO4) become less soluble with increasing temperature.
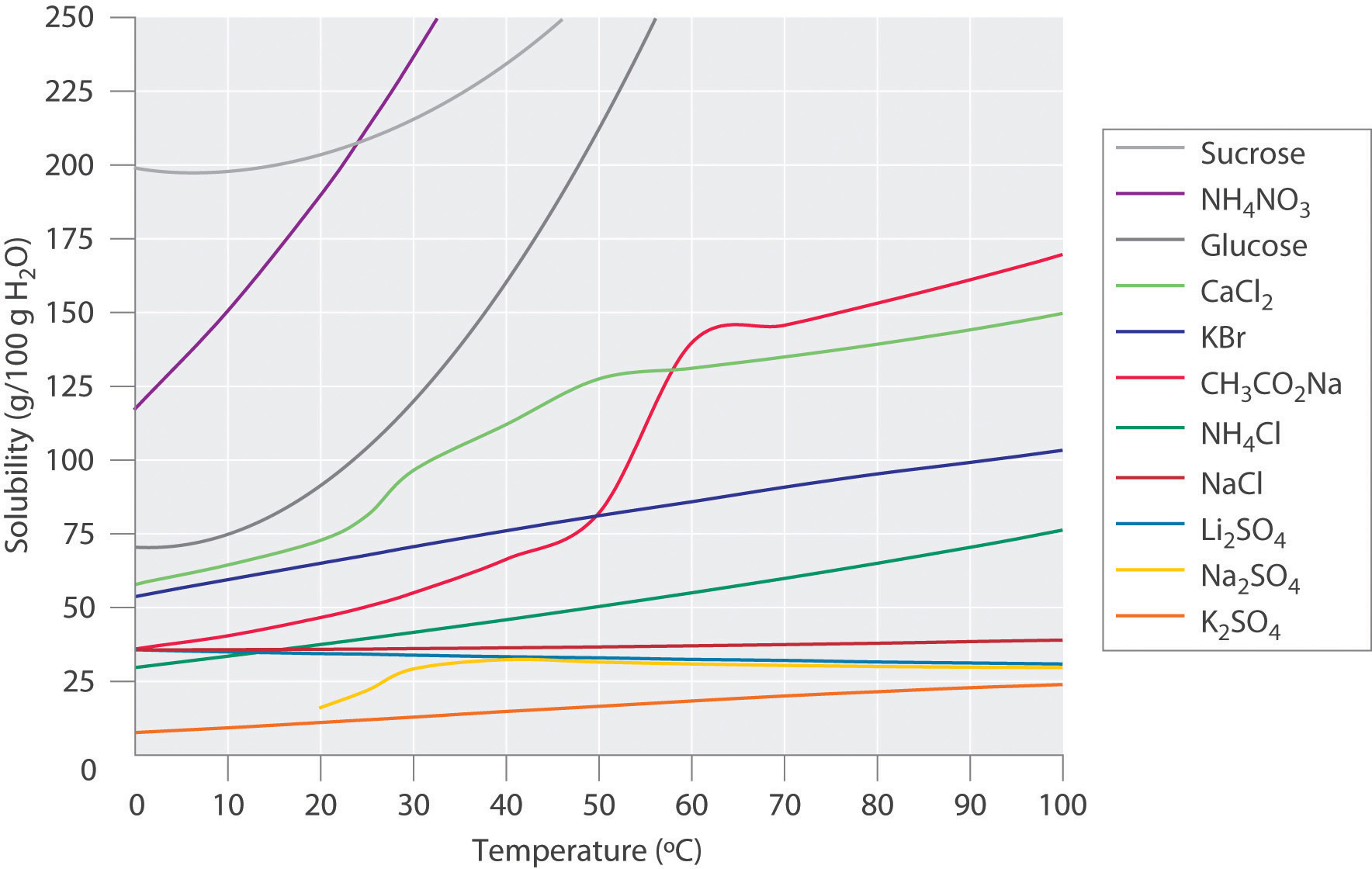
Figure 7.3 Solubilities of Several Inorganic and Organic Solids in Water as a Function of Temperature. Solubility may increase or decrease with temperature; the magnitude of this temperature dependence varies widely among compounds.
The variation of solubility with temperature has been measured for a wide range of compounds, and the results are published in many standard reference books. Chemists are often able to use this information to separate the components of a mixture by fractional crystallization, the separation of compounds on the basis of their solubilities in a given solvent. For example, if we have a mixture of 150 g of sodium acetate (CH3CO2Na) and 50 g of KBr, we can separate the two compounds by dissolving the mixture in 100 g of water at 80°C and then cooling the solution slowly to 0°C. According to the temperature curves in Figure 7.3, both compounds dissolve in water at 80°C, and all 50 g of KBr remains in solution at 0°C. Only about 36 g of CH3CO2Na are soluble in 100 g of water at 0°C, however, so approximately 114 g (150 g − 36 g) of CH3CO2Na crystallizes out on cooling. The crystals can then be separated by filtration. Thus fractional crystallization allows us to recover about 75% of the original CH3CO2Na in essentially pure form in only one step.
Fractional crystallization is a common technique for purifying compounds as diverse as those shown in Figure 7.3 and from antibiotics to enzymes. For the technique to work properly, the compound of interest must be more soluble at high temperature than at low temperature, so that lowering the temperature causes it to crystallize out of solution. In addition, the impurities must be more soluble than the compound of interest (as was KBr in this example) and preferably present in relatively small amounts.
The solubility of gases in liquids is much more predictable. The solubility of gases in liquids decreases with increasing temperature, as shown in Figure 7.4. Attractive intermolecular interactions in the gas phase are essentially zero for most substances, because the molecules are so far apart when in the gaseous form. When a gas dissolves, it does so because its molecules interact with solvent molecules. Heat is released when these new attractive forces form. Thus, if external heat is added to the system, it overcomes the attractive forces between the gas and the solvent molecules and decreases the solubility of the gas.
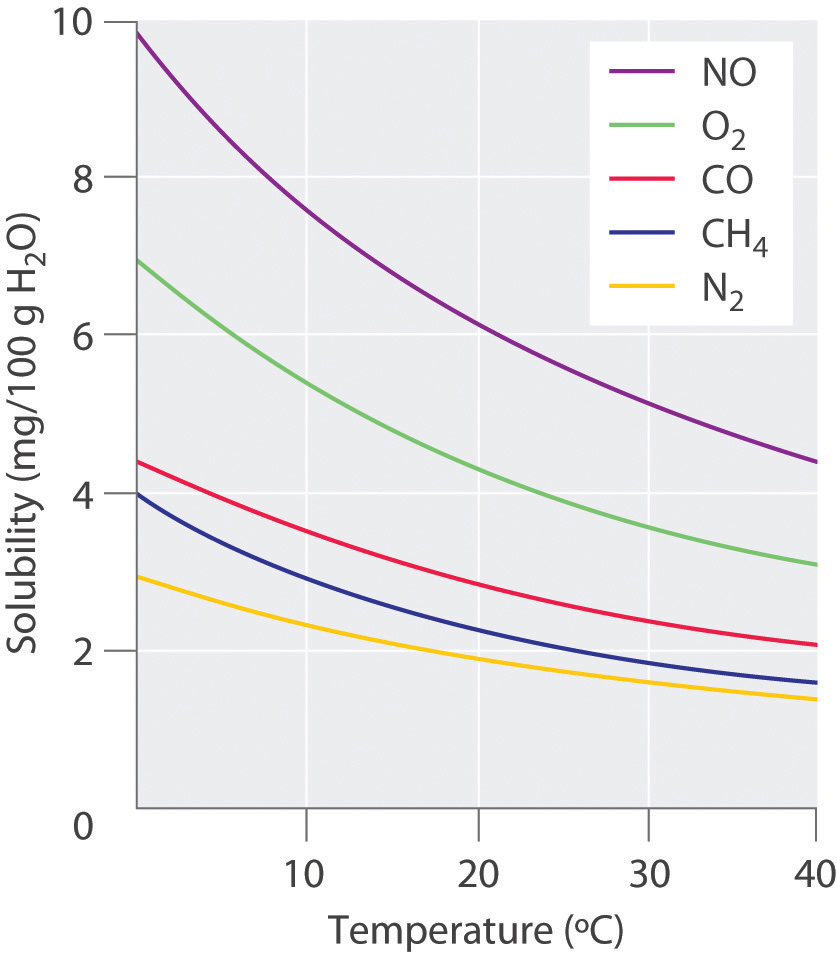
Figure 7.4 Solubilities of Several Common Gases in Water as a Function of Temperature at Partial Pressure of 1 atm. The solubilities of gases decrease with increasing temperature.
The decrease in the solubilities of gases at higher temperatures has both practical and environmental implications. Anyone who routinely boils water in a teapot or electric kettle knows that a white or gray deposit builds up on the inside and must eventually be removed. The same phenomenon occurs on a much larger scale in the giant boilers used to supply hot water or steam for industrial applications, where it is called “boiler scale,” a deposit that can seriously decrease the capacity of hot water pipes (Figure 7.5). The problem is not a uniquely modern one: aqueducts that were built by the Romans 2000 years ago to carry cold water from alpine regions to warmer, drier regions in southern France were clogged by similar deposits. The chemistry behind the formation of these deposits is moderately complex, but the driving force is the loss of dissolved carbon dioxide (CO2) from solution. Hard water contains dissolved Ca2+ and HCO3− (bicarbonate) ions. Calcium bicarbonate [Ca(HCO3)2] is rather soluble in water, but calcium carbonate (CaCO3) is quite insoluble. A solution of bicarbonate ions can react to form carbon dioxide, carbonate ion, and water:
Heating the solution decreases the solubility of CO2, which escapes into the gas phase above the solution. In the presence of calcium ions, the carbonate ions precipitate as insoluble calcium carbonate, the major component of boiler scale.

Figure 7.5 Boiler Scale in a Water Pipe. Calcium carbonate (CaCO3) deposits in hot water pipes can significantly reduce pipe capacity. These deposits, called boiler scale, form when dissolved CO2 is driven into the gas phase at high temperatures.
In thermal pollution, lake or river water that is used to cool an industrial reactor or a power plant is returned to the environment at a higher temperature than normal. Because of the reduced solubility of O2 at higher temperatures (Figure 7.4), the warmer water contains less dissolved oxygen than the water did when it entered the plant. Fish and other aquatic organisms that need dissolved oxygen to live can literally suffocate if the oxygen concentration of their habitat is too low. Because the warm, oxygen-depleted water is less dense, it tends to float on top of the cooler, denser, more oxygen-rich water in the lake or river, forming a barrier that prevents atmospheric oxygen from dissolving. Eventually even deep lakes can be suffocated if the problem is not corrected. Additionally, most fish and other nonmammalian aquatic organisms are cold-blooded, which means that their body temperature is the same as the temperature of their environment. Temperatures substantially greater than the normal range can lead to severe stress or even death. Cooling systems for power plants and other facilities must be designed to minimize any adverse effects on the temperatures of surrounding bodies of water. In the Pacific Northwest, salmonid populations are extremely susceptible to changes in water temperature. Within these population, optimal water temperatures are between 12.8 and 17.8 oC (55-65 oF). In addition to reduced oxygen levels, salmon populations are much more susceptible to disease, predation, and parasite infections at higher water temperatures. Thus, thermal pollution and global climate change are creating real challenges to the survival and maintenance of these species. For more information on the effects of rising temperatures on salmonid populations visit the State of Washington’s Focus Publication.
A similar effect is seen in the rising temperatures of bodies of water such as the Chesapeake Bay, the largest estuary in North America, where global warming has been implicated as the cause. For each 1.5°C that the bay’s water warms, the capacity of water to dissolve oxygen decreases by about 1.1%. Many marine species that are at the southern limit of their distributions have shifted their populations farther north. In 2005, the eelgrass, which forms an important nursery habitat for fish and shellfish, disappeared from much of the bay following record high water temperatures. Presumably, decreased oxygen levels decreased populations of clams and other filter feeders, which then decreased light transmission to allow the eelsgrass to grow. The complex relationships in ecosystems such as the Chesapeake Bay are especially sensitive to temperature fluctuations that cause a deterioration of habitat quality.
(Back to the Top)
7.5 Effects of Pressure on the Solubility of Gases: Henry’s Law
External pressure has very little effect on the solubility of liquids and solids. In contrast, the solubility of gases increases as the partial pressure of the gas above a solution increases. This point is illustrated in Figure 7.6, which shows the effect of increased pressure on the dynamic equilibrium that is established between the dissolved gas molecules in solution and the molecules in the gas phase above the solution. Because the concentration of molecules in the gas phase increases with increasing pressure, the concentration of dissolved gas molecules in the solution at equilibrium is also higher at higher pressures.
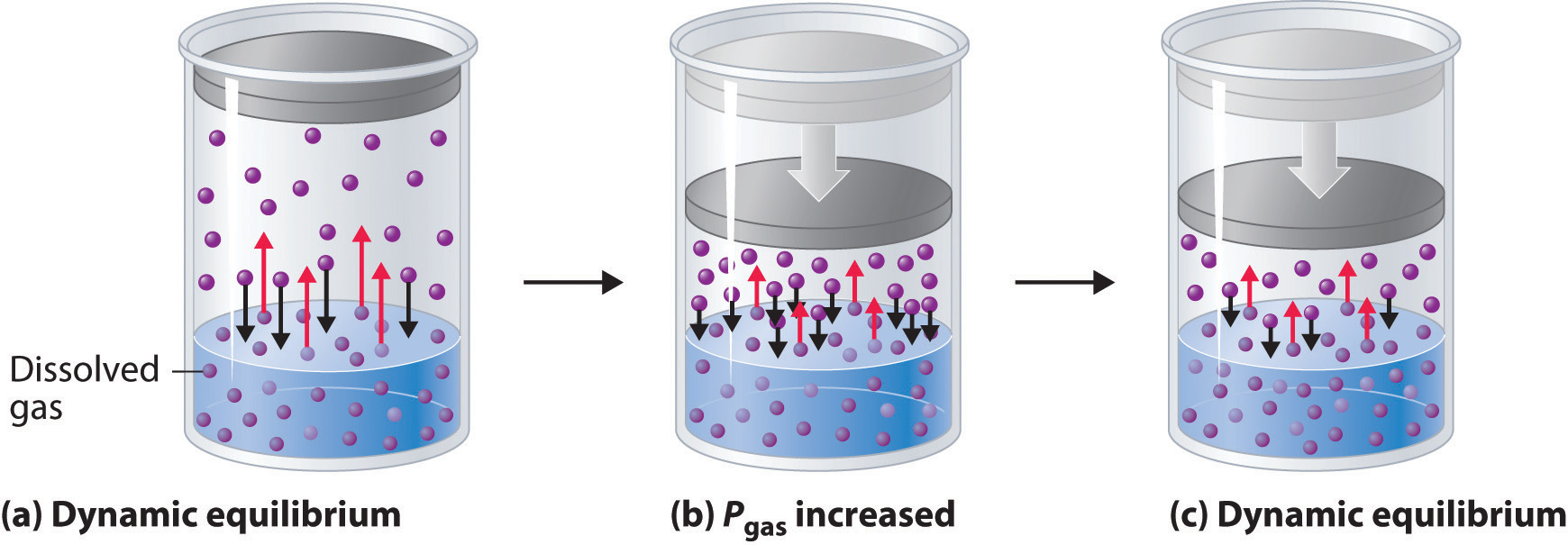
Figure 7.6 A Model Depicting Why the Solubility of a Gas Increases as the Partial Pressure Increases at Constant Temperature. (a) When a gas comes in contact with a pure liquid, some of the gas molecules (purple spheres) collide with the surface of the liquid and dissolve. When the concentration of dissolved gas molecules has increased so that the rate at which gas molecules escape into the gas phase is the same as the rate at which they dissolve, a dynamic equilibrium has been established, as depicted here. (b) Increasing the pressure of the gas increases the number of molecules of gas per unit volume, which increases the rate at which gas molecules collide with the surface of the liquid and dissolve. (c) As additional gas molecules dissolve at the higher pressure, the concentration of dissolved gas increases until a new dynamic equilibrium is established.
The relationship between pressure and the solubility of a gas is described quantitatively by Henry’s law, which is named for its discoverer, the English physician and chemist, William Henry (1775–1836):
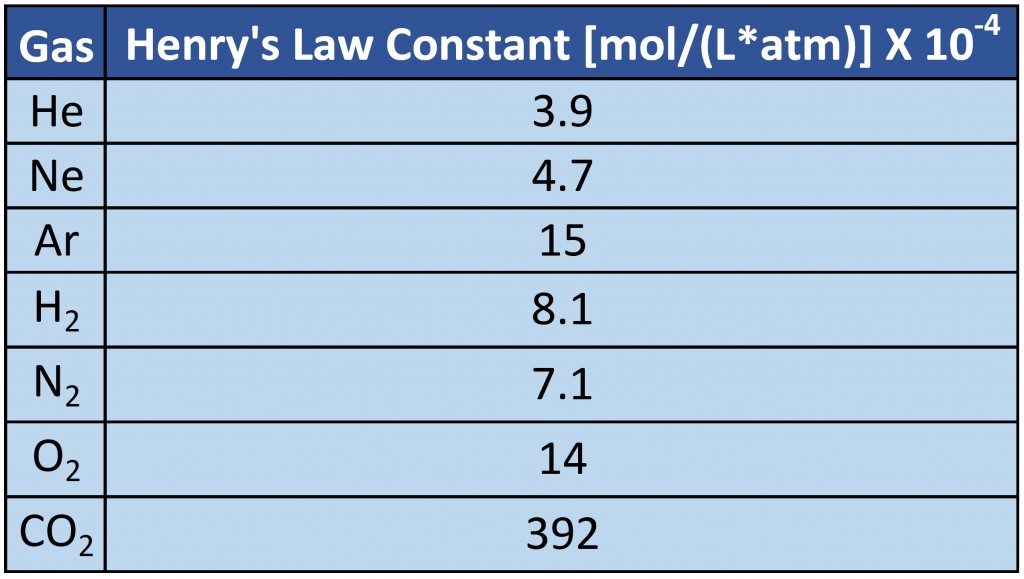
where C is the concentration of dissolved gas at equilibrium, P is the partial pressure of the gas, and k is the Henry’s law constant, which must be determined experimentally for each combination of gas, solvent, and temperature. Although the gas concentration may be expressed in any convenient units, we will use molarity exclusively. The units of the Henry’s law constant are therefore mol/(L·atm) = M/atm. Values of the Henry’s law constants for solutions of several gases in water at 20°C are listed in Table 7.2
Video Tutorial on Henry’s Law from Kahn Academy
All Khan Academy content is available for free at www.khanacademy.org
As the data in Table 7.2 demonstrate, the concentration of a dissolved gas in water at a given pressure depends strongly on its physical properties. For a series of related substances, London dispersion forces increase as molecular mass increases. Thus among the elements of group 18, the Henry’s law constants increase smoothly from He to Ne to Ar. The table also shows that O2 is almost twice as soluble as N2. Although London dispersion forces are too weak to explain such a large difference, O2 is paramagnetic and hence more polarizable than N2, which explains its high solubility. (Note: When a substance is paramagnetic it is very weakly attracted by the poles of a magnet, but does not retain any permanent magnetism).
Table 7.2 Henry’s Law Constants for Selected Gases in Water at 20°C
The partial pressure of a gas can be expressed as concentration by writing Henry’s Law as Pgas = C/k. This is important in many aspects of life including medicine where blood gases, like oxygen and carbon dioxide are commonly measured. Since partial pressure and concentration are directly proportional, if the partial pressure of a gas changes while the temperature remains constant, the new concentration of the gas within the liquid can be easily calculated using the following equation:
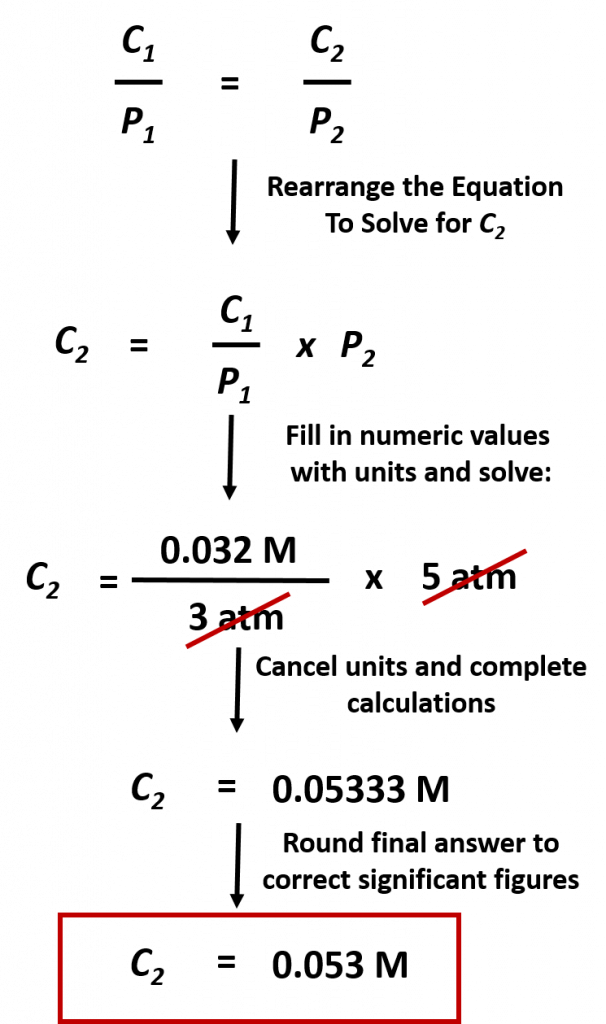
Where C1 and P1 are the concentration and partial pressure, respectively, of the gas at the initial condition, and C2 and P2 are the concentration and partial pressure, respectively, of the gas at the final condition. For example:
Practice Problem: The concentration of CO2 in a solution is 0.032 M at 3.0 atm. What is the concentration of CO2 at 5.0 atm of pressure?
Solution: To address this problem, first we must identify what we want to find. This is the concentration of CO2 at 5.0 atm of pressure. These two values represent C2 = ?? and P2 = 5.0 atm. At this point it will be easiest to rearrange our equation above to solve for C2. Next we need to identify the starting conditions, C1 = 0.032 M and P1 = 3.0 atm. Then we can plug that values into the equation and solve for C2 :
Gases that react chemically with water, such as HCl and the other hydrogen halides, H2S, and NH3, do not obey Henry’s law; all of these gases are much more soluble than predicted by Henry’s law. For example, HCl reacts with water to give H+(aq) and Cl−(aq), not dissolved HCl molecules, and its dissociation into ions results in a much higher solubility than expected for a neutral molecule. Overall, gases that react with water do not obey Henry’s Law.
Note the Pattern
Henry’s law has important applications. For example, bubbles of CO2 form as soon as a carbonated beverage is opened because the drink was bottled under CO2 at a pressure greater than 1 atm. When the bottle is opened, the pressure of CO2 above the solution drops rapidly, and some of the dissolved gas escapes from the solution as bubbles. Henry’s law also explains why scuba divers have to be careful to ascend to the surface slowly after a dive if they are breathing compressed air. At the higher pressures under water, more N2 from the air dissolves in the diver’s internal fluids. If the diver ascends too quickly, the rapid pressure change causes small bubbles of N2 to form throughout the body, a condition known as “the bends.” These bubbles can block the flow of blood through the small blood vessels, causing great pain and even proving fatal in some cases.
Due to the low Henry’s law constant for O2 in water, the levels of dissolved oxygen in water are too low to support the energy needs of multicellular organisms, including humans. To increase the O2 concentration in internal fluids, organisms synthesize highly soluble carrier molecules that bind O2 reversibly. For example, human red blood cells contain a protein called hemoglobin that specifically binds O2 and facilitates its transport from the lungs to the tissues, where it is used to oxidize food molecules to provide energy. The concentration of hemoglobin in normal blood is about 2.2 mM, and each hemoglobin molecule can bind four O2 molecules. Although the concentration of dissolved O2 in blood serum at 37°C (normal body temperature) is only 0.010 mM, the total dissolved O2 concentration is 8.8 mM, almost a thousand times greater than would be possible without hemoglobin. Synthetic oxygen carriers based on fluorinated alkanes have been developed for use as an emergency replacement for whole blood. Unlike donated blood, these “blood substitutes” do not require refrigeration and have a long shelf life. Their very high Henry’s law constants for O2 result in dissolved oxygen concentrations comparable to those in normal blood.
(Back to the Top)
7.6 Solid Hydrates:
Some ionic solids will accept a small number of water molecules into their crystal lattice structure and remain in a solid state. These solids are called solid hydrates. Solid hydrates contain water molecules combined in a definite ratio as an integral part of the crystal that are either bound to a metal center or that have crystallized with the metal complex. Such hydrates are also said to contain water of crystallization or water of hydration.
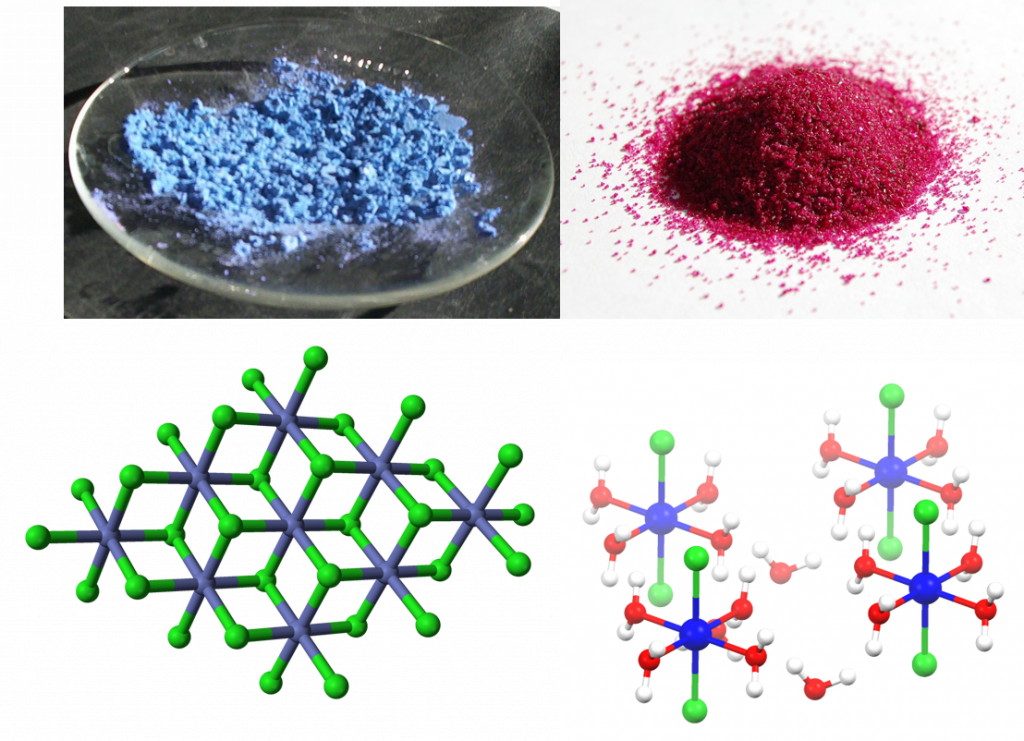
A colorful example is cobalt(II) chloride, which turns from blue to red upon hydration, and can therefore be used as a water indicator.
Figure 7.7: Cobalt chloride as an example of a solid hydrate. Anhydrous cobalt chloride (upper left) and it’s crystal lattice structure (lower left) compared with cobalt chloride hexahydrate (upper right) and it’s crystal lattice (lower right). Notice that the water molecules shown in red (oxygen) and white (hydrogen) are integrated into the crystal lattice of the cobalt (II) chloride, shown in blue (cobalt) and green (chloride), based on polarity. The partially negative oxygen atoms are attracted to the positively charged cobalt while the partially positive hydrogen atoms are attracted to the negatively charged chloride ions. Images provided by Wikipedia Commons (upper left and lower left), Benjah-bmm27 (upper right), and Smokefoot (lower right)
The notation used to represent a solid hydrate is: “hydrated compound⋅nH2O“, where n is the number of water molecules per formula unit of the salt. The n is usually a low integer, though it is possible for fractional values to occur. For example, in a monohydrate n is one, and in a hexahydrate n is 6. For the example in Figure 7.7, the hydrated cobalt chloride would be designated: “cobalt (II) chloride⋅6H2O”. Numerical prefixes of Greek origin that are used to designate solid hydrates are:
- Hemi – 1/2
- Mono – 1
- Sesqui – 1½
- Di – 2
- Tri – 3
- Tetra – 4
- Penta – 5
- Hexa – 6
- Hepta – 7
- Octa – 8
- Nona – 9
- Deca – 10
- Undeca – 11
- Dodeca – 12
A hydrate which has lost water is referred to as an anhydride; the remaining water, if any exists, can only be removed with very strong heating. A substance that does not contain any water is referred to as anhydrous. Some anhydrous compounds are hydrated so easily that they will pull water out of the atmosphere and become hydrated. These substances are said to be hygroscopic and can be used as drying agents or desiccants.
(Back to the Top)
7.7 Solution Concentration
In chemistry, concentration is defined as the abundance of a constituent divided by the total volume of a mixture. All of us have a qualitative idea of what is meant by concentration. Anyone who has made instant coffee or lemonade knows that too much powder gives a strongly flavored, highly concentrated drink, whereas too little results in a dilute solution that may be hard to distinguish from water. Quantitatively, the concentration of a solution describes the quantity of a solute that is contained in a particular quantity of that solution. Knowing the concentration of solutes is important in controlling the stoichiometry of reactants for reactions that occur in solution, and are critical for many aspects of our lives, from measuring the correct dose of medicine to detecting chemical pollutants like lead and arsenic. Chemists use many different ways to define concentrations. In this section, we will cover the most common ways of presenting solution concentration. These include: Molarity and Parts Per Solutions.
7.7.1 Molarity
The most common unit of concentration is molarity, which is also the most useful for calculations involving the stoichiometry of reactions in solution. The molarity (M) of a solution is the number of moles of solute present in exactly 1 L of solution.
The units of molarity are therefore moles per liter of solution (mol/L), abbreviated as M. Note that the volume indicated is the total volume of the solution and includes both the solute and the solvent. For example, an aqueous solution that contains 1 mol (342 g) of sucrose in enough water to give a final volume of 1.00 L has a sucrose concentration of 1.00 mol/L or 1.00 M. In chemical notation, square brackets around the name or formula of the solute represent the concentration of a solute. So
[sucrose] = 1.00 M
is read as “the concentration of sucrose is 1.00 molar.” The equation above can be used to calculate how much solute is required to make any amount of a desired solution.
Example Problem:
Calculate the number of moles of sodium hydroxide (NaOH) needed to make 2.50 L of 0.100 M NaOH.
Given: (1) identity of solute = NaOH, (2) volume = 2.50 L, and (3) molarity of solution = 0.100 mol/L (Note: when calculating problems always write out the units of molarity as mol/L, rather than M. This will allow you to cancel out your units when doing the calculation.)
Asked for: amount of solute in moles
Strategy: (1) Rearrange the equation above to solve for the desired unit, in this case for moles. (2) Double check all the units in the equation and make sure they match. Perform any conversions that are needed so that the units match. (3) Fill in values appropriately and do the math.
Solution:
(1) Rearrange the equation above to solve for moles.
(2) Double check all the units in the equation and make sure they match.
The given values for this equation are the volume 2.50 L and the molarity 0.100 mol/L. The volume units for both of these numbers are in Liters (L) and thus, match. Therefore, no conversions need to be made.
(3) Fill in values appropriately and do the math.
Preparation of Solutions
Figure 7.8 illustrates the procedure for making a solution of cobalt(II) chloride dihydrate in ethanol. Note that the volume of the solvent is not specified. Since the solute occupies space in the solution, the volume of the solvent needed is less than the desired total volume of solution.

Figure 7.8: Preparation of a Solution of Known Concentration Using a Solid Solute. To make a solution, start by addition a portion of the solvent to the flask. Next, weigh out the appropriate amount of solute and slowly add it to the solvent. Once it is dissolved in the solvent, the volume of the solution can be brought up to the final solution volume. For the volumetric flask shown, this is indicated by the black line in the neck of the flask. In this case, it indicates 500 mL of solution. Volumetric flasks exist in many different sizes to accommodate different solution volumes. Graduated cylinders can also be used to accurately bring a solution to its final volume. Other glassware, including beakers and Erlenmeyer flasks are not accurate enough to make most solutions.
Example Molarity Calculation
The solution in Figure 7.8 contains 10.0 g of cobalt(II) chloride dihydrate, CoCl2·2H2O, in enough ethanol to make exactly 500 mL of solution. What is the molar concentration of CoCl2·2H2O?
Given: mass of solute and volume of solution
Asked for: concentration (M)
Strategy:
1. We know that Molarity equals moles/Liter
2. To calculate Molarity, we need to express:
- the mass in the form of moles
- the volume in the form of Liters
- Plug both into the equation above and calculate
Solution:
- Converting the mass into moles. We can use the molar mass to convert the grams of CoCl2·2H2O to moles.
- The molar mass of CoCl2·2H2O is 165.87 g/mol (and includes the two water molecules as they are part of the crystal lattice structure of this solid hydrate!)
2. Convert the volume into Liters
7.7.2 Parts Per Solutions
In the consumer and industrial world, the most common method of expressing the concentration is based on the quantity of solute in a fixed quantity of solution. The “quantities” referred to here can be expressed in mass, in volume, or both (i.e., the mass of solute in a given volume of solution.) In order to distinguish among these possibilities, the abbreviations (m/m), (v/v) and (m/v) are used.
In most applied fields of Chemistry, (m/m) measure is often used, whereas in clinical chemistry, (m/v) is commonly used, with mass expressed in grams and volume in mL.
One of the more common ways to express such concentrations as “parts per 100“, which we all know as “percent“. “Cent” is the Latin-derived prefix relating to the number 100
(L. centum), as in century or centennial. It also denotes 1/100th (from L. centesimus) as in centimeter and the monetary unit cent. Percent solutions define the quantity of a solute that is dissolved in a quantity of solution multiplied by 100. Percent solutions can be expressed in terms of mass solute per mass solution (m/m%), or mass solute per volume of solution (m/v%), or volume of solute per volume of solution (v/v%). When making a percent solution, it is important to indicate what units are being used, so that others can also make the solution properly. Also, recall that the solution is the sum of both the solvent and the solute when you are performing percent calculations.
Solution = Solute + Solvent
Thus, the following equation can be used when calculating percent solutions:
Example 1:
As an example, a 7.0% v/v solution of ethanol in water, would contain 7 mL of ethanol in a total of 100 mL of solution. How much water is in the solution?
In this problem, we know that the:
Solution = Solute + Solvent
Thus, we can fill in the values and then solve for the unknown.
100 mL = 7 mL + X mL of Solvent (in this case water)
shifting the 7 over to the other side, we can see that:
100 mL – 7 mL = 93 mL H2O
Example 2
What is the (m/v)% of a solution if 24.0 g of sucrose is dissolved in a total solution of 243 mL?
Example 3
How many grams of NaCl are required to make 625 mL of a 13.5% solution?
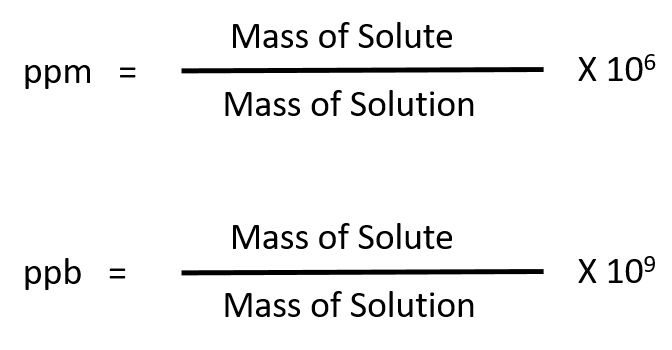
For more dilute solutions, parts per million (106 ppm) and parts per billion (109; ppb) are used. These terms are widely employed to express the amounts of trace pollutants in the environment.
Like percentage (“part per hundred”) units, ppm and ppb may be defined in terms of masses, volumes, or mixed mass-volume units. There are also ppm and ppb units defined with respect to numbers of atoms and molecules.
The mass-based definitions of ppm and ppb are given here:
Both ppm and ppb are convenient units for reporting the concentrations of pollutants and other trace contaminants in water. Concentrations of these contaminants are typically very low in treated and natural waters, and their levels cannot exceed relatively low concentration thresholds without causing adverse effects on health and wildlife. For example, the EPA has identified the maximum safe level of fluoride ion in tap water to be 4 ppm. Inline water filters are designed to reduce the concentration of fluoride and several other trace-level contaminants in tap water (Figure 7.9).
Figure 7.9. (a) In some areas, trace-level concentrations of contaminants can render unfiltered tap water unsafe for drinking and cooking. (b) Inline water filters reduce the concentration of solutes in tap water. (credit a: modification of work by Jenn Durfey; credit b: modification of work by “vastateparkstaff”/Wikimedia commons
When reporting contaminants like lead in drinking water, ppm and ppb concentrations are often reported in mixed unit values of mass/volume. This can be very useful as it is easier for us to think about water in terms of its volume, rather than by its mass. In addition, the density of water is 1.0 g/mL or 1.0 mg/0.001 mL which makes the conversion between the two units easier. For example, if we find that there is lead contamination in water of 4 ppm, this would mean that there are:
7.74 Equivalents
Concentrations of ionic solutes are occasionally expressed in units called equivalents (Eq). One equivalent equals 1 mol of positive or negative charge. Thus, 1 mol/L of Na+(aq) is also 1 Eq/L because sodium has a 1+ charge. A 1 mol/L solution of Ca2+(aq) ions has a concentration of 2 Eq/L because calcium has a 2+ charge. Dilute solutions may be expressed in milliequivalents (mEq)—for example, human blood plasma has a total concentration of about 150 mEq/L.
In a more formal definition, the equivalent is the amount of a substance needed to do one of the following:
- react with or supply one mole of hydrogen ions (H+) in an acid–base reaction
- react with or supply one mole of electrons in a redox reaction.
By this definition, an equivalent is the number of moles of an ion in a solution, multiplied by the valence of that ion. If 1 mol of NaCl and 1 mol of CaCl2 dissolve in a solution, there is 1 equiv Na, 2 equiv Ca, and 3 equiv Cl in that solution. (The valence of calcium is 2, so for that ion you have 1 mole and 2 equivalents.)
(Back to the Top)
7.8 Dilutions
A solution of a desired concentration can also be prepared by diluting a small volume of a more concentrated solution with additional solvent. A stock solution, which is a prepared solution of known concentration, is often used for this purpose. Diluting a stock solution is preferred when making solutions of very weak concentrations, because the alternative method, weighing out tiny amounts of solute, can be difficult to carry out with a high degree of accuracy. Dilution is also used to prepare solutions from substances that are sold as concentrated aqueous solutions, such as strong acids.
The procedure for preparing a solution of known concentration from a stock solution is shown in Figure 7.10. It requires calculating the amount of solute desired in the final volume of the more dilute solution and then calculating the volume of the stock solution that contains this amount of solute. Remember that diluting a given quantity of stock solution with solvent does not change the amount of solute present, only the volume of the solution is changing. The relationship between the volume and concentration of the stock solution and the volume and concentration of the desired diluted solution can therefore be expressed mathematically as:
Where Ms is the concentration of the stock solution, Vs is the volume of the stock solution, Md is the concentration of the diluted solution, and Vd is the volume of the diluted solution.
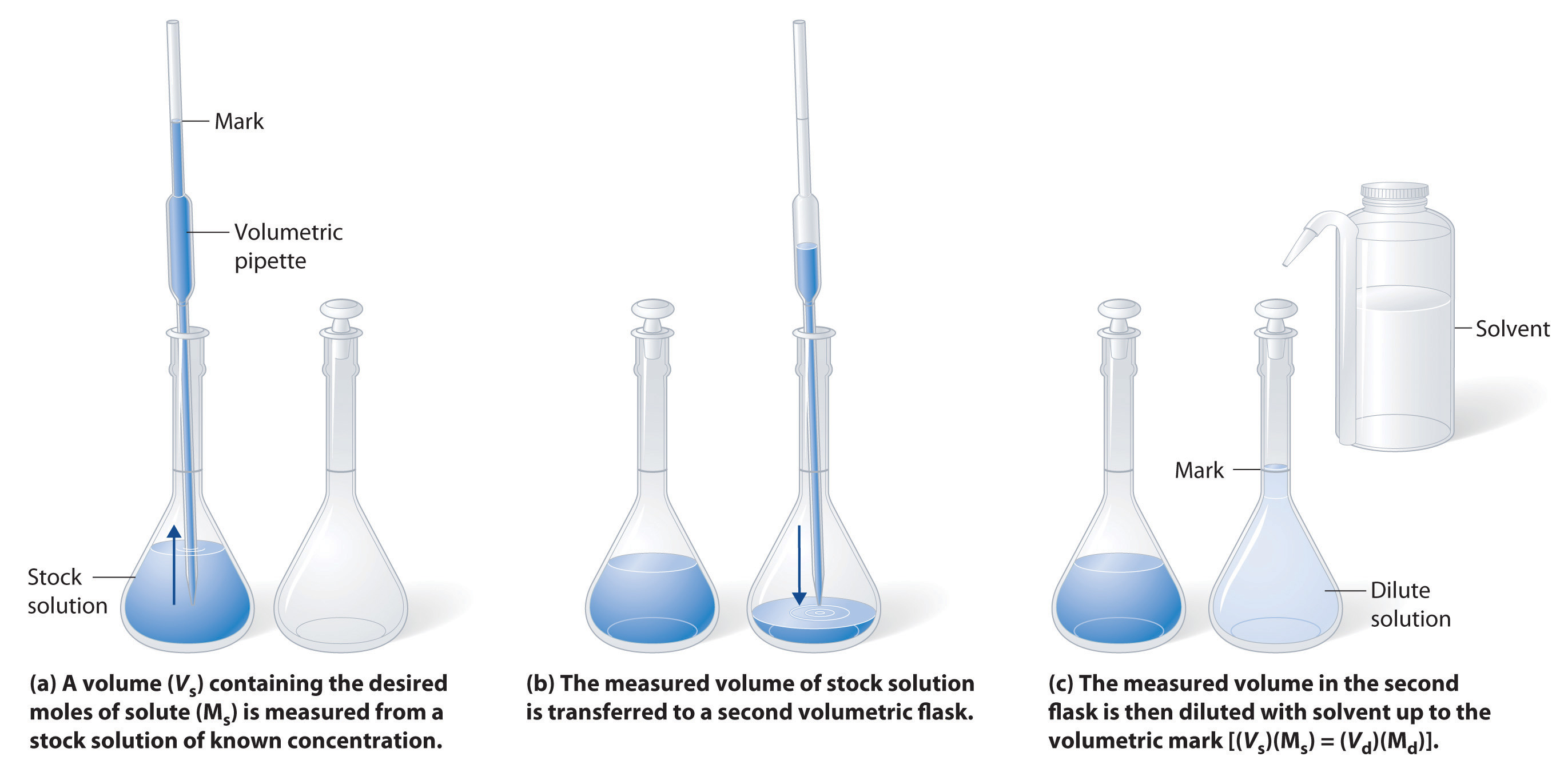
Figure 7.10 Preparation of a Solution of Known Concentration by Diluting a Stock Solution. (a) A volume (Vs) containing the desired amount of solute (Ms) is measured from a stock solution of known concentration. (b) The measured volume of stock solution is transferred to a second volumetric flask. (c) The measured volume in the second flask is then diluted with solvent up to the volumetric mark [(Vs)(Ms) = (Vd)(Md)].
Example of Dilution Calculations
What volume of a 3.00 M glucose stock solution is necessary to prepare 2500 mL of 0.400 M solution?
Given: volume and molarity of dilute solution, and molarity of stock solution
Asked for: volume of stock solution
Strategy and Solution:
For Dilution problems, as long as you know 3 of the variables, you can solve for the 4th variable.
- Start by rearranging the equation to solve for the variable that you want to find. In this case, you want to find the volume of the stock solution, Vs
2. Next, check to make sure that like terms have the same units. For example, Md and Ms are both concentrations, thus, to be able to perform the calculations, they should be in the same unit (in this case they are both listed in Molarity). If the concentrations were different, say one was given in Molarity and the other in percent or one was in Molarity and the other was in Millimolarity, one of the terms would need to be converted so that they match. That way, the units will cancel out and leave you with units of volume, in this case.
3. Finally, fill in the equation with known values and calculate the final answer.
Note that if 333mL of stock solution is needed, that you can also calculate the amount of solvent needed to make the final dilution. (Total volume – volume of stock solution = volume of solvent needed for the final dilution. In this case 2,500 mL – 333 mL = 2,167 mL of water needed to make the final dilution (this should be done in a graduated cylinder or volumetric flask).
(Back to the Top)
7.9 Ion Concentrations in Solution
Thus far, we have been discussing the concentration of the overall solution in terms of total solute divided by the volume of the solution. Let’s consider in more detail exactly what that means when considering ionic and covalent compounds. When ionic compounds dissolve in a solution, they break apart into their ionic state. Cations and anions associate with the polar water molecules. Recall that solutions that contain ions are called electrolyotes, due to their ability to conduct electricity. For example, ammonium dichromate (NH4)2Cr2O7 is an ionic compound that contains two NH4+ ions and one Cr2O72− ion per formula unit. Like other ionic compounds, it is a strong electrolyte that dissociates in aqueous solution to give hydrated NH4+ and Cr2O72− ions. If we consider this this solution mathematically, we can see that for every ammonium dichromate molecule that dissolves, there will be three resulting ions that form (the two NH4+ ions and the one Cr2O72− ion). This can also be thought of on a larger molar scale. When 1 mole of (NH4)2Cr2O7 is dissolved, it results in 3 moles of ions (1 mol of Cr2O72− anions and 2 mol of NH4+ cations) within the solution (Figure 7.11). To discuss the relationship between the concentration of a solution and the resulting number of ions, the term equivalents is used.
One equivalent is defined as the amount of an ionic compound that provides 1 mole of electrical charge (+ or -). It is calculated by dividing the molarity of the solution by the total charge created in the solution.
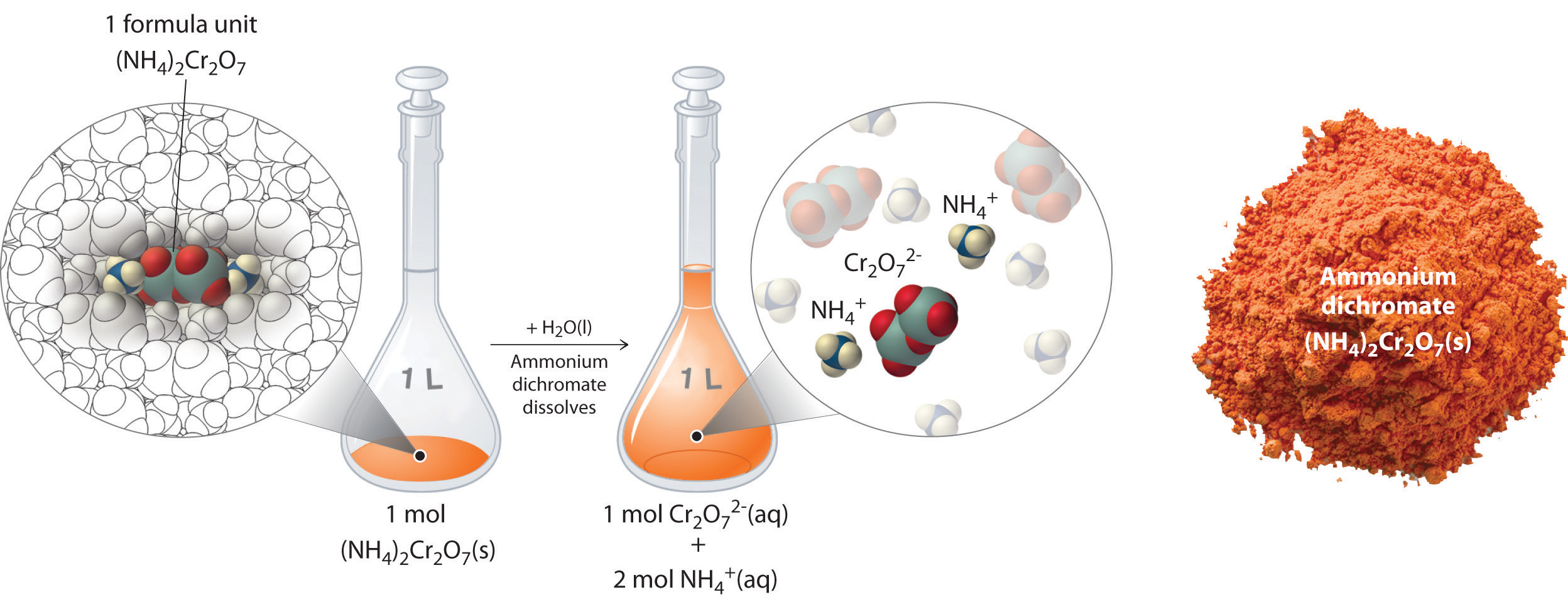
Figure 7.11 Dissolution of 1 mol of an Ioncic Compound. Dissoliving 1 mol of ammonium dichromate formula units in water produces 1 mol of Cr2O72− anions and 2 mol of NH4+ cations. (Water molecules are omitted from a molecular view of the solution for clarity.)
When we carry out a chemical reaction using a solution of a salt such as ammonium dichromate, we need to know the concentration of each ion present in the solution. If a solution contains 1.43 M (NH4)2Cr2O7, then the concentration of Cr2O72− must also be 1.43 M because there is one Cr2O72− ion per formula unit. However, there are two NH4+ ions per formula unit, so the concentration of NH4+ ions is 2 × 1.43 M = 2.86 M. Because each formula unit of (NH4)2Cr2O7 produces three ions when dissolved in water (2NH4+ + 1Cr2O72−), the total concentration of ions in the solution is 3 × 1.43 M = 4.29 M. The equivalent value of (NH4)2Cr2O7 can then be calculated by dividing 1.43 M by 4.29 M, yielding 0.333 equivalents. Thus, for (NH4)2Cr2O7, dissolving 0.333 moles of the compound will yield 1 mole of ions in the solution.
Example 1
What are the concentrations of all ionic species derived from the solutes in these aqueous solutions?
- 0.21 M NaOH
- 3.7 M (CH3)CHOH
- 0.032 M In(NO3)3
Given: molarity
Asked for: concentrations
Strategy:
A Classify each compound as either a strong electrolyte or a nonelectrolyte.
B If the compound is a nonelectrolyte, its concentration is the same as the molarity of the solution. If the compound is a strong electrolyte, determine the number of each ion contained in one formula unit. Find the concentration of each species by multiplying the number of each ion by the molarity of the solution.
Solution:
1. 0.21 M NaOH
A Sodium hydroxide is an ionic compound that is a strong electrolyte (and a strong base) in aqueous solution:
B Because each formula unit of NaOH produces one Na+ ion and one OH− ion, the concentration of each ion is the same as the concentration of NaOH: [Na+] = 0.21 M and [OH−] = 0.21
2. 3.7 M (CH3)CHOH
A The formula (CH3)2CHOH represents 2-propanol (isopropyl alcohol) and contains the –OH group, so it is an alcohol. Recall from Section 4.1 “Aqueous Solutions” that alcohols are covalent compounthat dissolve in water to give solutions of neutral molecules. Thus alcohols are nonelectrolytes
B The only solute species in solution is therefore (CH3)2CHOH molecules, so [(CH3)2CHOH] = 3.7 M
3. 0.032 M In(NO3)3
A Indium nitrate is an ionic compound that contains In3+ ions and NO3− ions, so we expect it to behave like a strong electrolyte in aqueous solution
B One formula unit of In(NO3)3 produces one In3+ ion and three NO3− ions, so a 0.032 M In(NO3)3 solution contains 0.032 M In3+ and 3 × 0.032 M = 0.096 M NO3–—that is, [In3+] = 0.032 M and [NO3−] = 0.096 M
(Back to the Top)
7.10 Summary
To ensure that you understand the material in this chapter, you should review the meanings of the bold terms in the following summary and ask yourself how they relate to the topics in the chapter.
A solution is a homogeneous mixture. The major component is the solvent, while the minor component is the solute. Solutions can have any phase; for example, an alloy is a solid solution. Solutes are soluble or insoluble, meaning they dissolve or do not dissolve in a particular solvent. The terms miscible and immiscible, instead of soluble and insoluble, are used for liquid solutes and solvents. The statement like dissolves like is a useful guide to predicting whether a solute will dissolve in a given solvent.
Dissolving occurs by solvation, the process in which particles of a solvent surround the individual particles of a solute, separating them to make a solution. For water solutions, the word hydration is used. If the solute is molecular, it dissolves into individual molecules. If the solute is ionic, the individual ions separate from each other, forming a solution that conducts electricity. Such solutions are called electrolytes. If the dissociation of ions is complete, the solution is a strong electrolyte. If the dissociation is only partial, the solution is a weak electrolyte. Solutions of molecules do not conduct electricity and are called nonelectrolytes.
The amount of solute in a solution is represented by the concentration of the solution. The maximum amount of solute that will dissolve in a given amount of solvent is called the solubility of the solute. Such solutions are saturated. Solutions that have less than the maximum amount are unsaturated. Most solutions are unsaturated, and there are various ways of stating their concentrations. Mass/mass percent, volume/volume percent, and mass/volume percent indicate the percentage of the overall solution that is solute. Parts per million (ppm) and parts per billion (ppb) are used to describe very small concentrations of a solute. Molarity, defined as the number of moles of solute per liter of solution, is a common concentration unit in the chemistry laboratory. Equivalents express concentrations in terms of moles of charge on ions. When a solution is diluted, we use the fact that the amount of solute remains constant to be able to determine the volume or concentration of the final diluted solution. Solutions of known concentration can be prepared either by dissolving a known mass of solute in a solvent and diluting to a desired final volume or by diluting the appropriate volume of a more concentrated solution (a stock solution) to the desired final volume.
Key Takeaway
- Solution concentrations are typically expressed as molarity and can be prepared by dissolving a known mass of solute in a solvent or diluting a stock solution.
Conceptual Problems
-
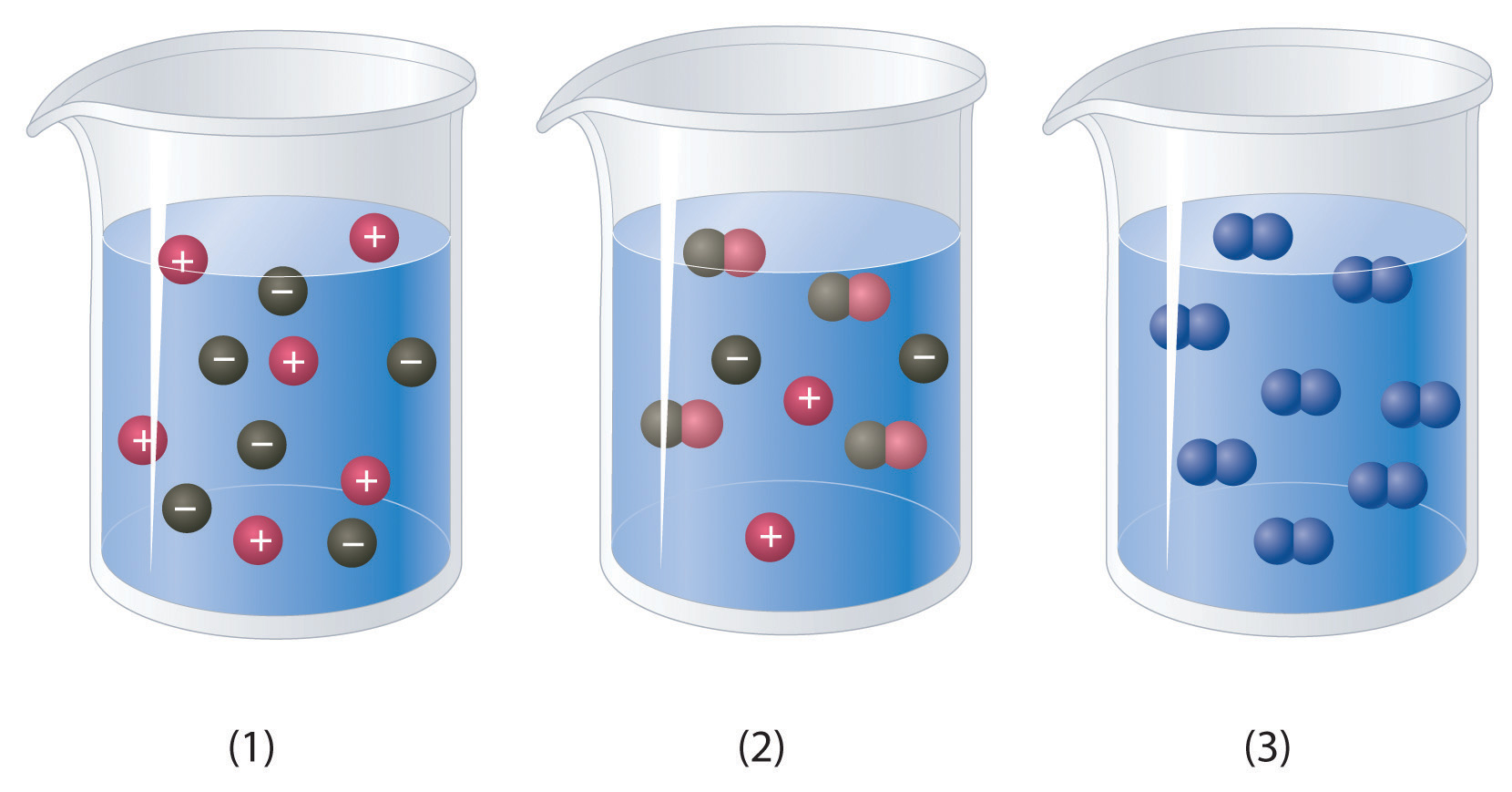
Which of the representations best corresponds to a 1 M aqueous solution of each compound? Justify your answers.
- NH3
- HF
- CH3CH2CH2OH
-
Na2SO4

-
Which of the representations shown in Problem 1 best corresponds to a 1 M aqueous solution of each compound? Justify your answers.
- CH3CO2H
- NaCl
- Na2S
- Na3PO4
- acetaldehyde
-
Would you expect a 1.0 M solution of CaCl2 to be a better conductor of electricity than a 1.0 M solution of NaCl? Why or why not?
-
An alternative way to define the concentration of a solution is molality, abbreviated m. Molality is defined as the number of moles of solute in 1 kg of solvent. How is this different from molarity? Would you expect a 1 M solution of sucrose to be more or less concentrated than a 1 m solution of sucrose? Explain your answer.
-
What are the advantages of using solutions for quantitative calculations?
Answer
-
a) NH3 is a weak base, which means that some of the molecules will accept a proton from water molecules causing them to dissociate into H+ and -OH ions. The H+ ion will associate with the NH3 to form NH4+. Thus this would look the most like beaker #2. b) HF is a weak acid even though F is strongly electronegative. This is because the H-F molecule can form strong hydrogen bonds with the water molecules and remain in a covalent bond that is harder to dissociate. Thus, beaker #2 is also a good choice for this molecule, as only some of the H-F will dissociate to H3O+ and F- ions. c) CH3CH2CH2OHis a covalent compound and will not dissociate to any appreciable extent, thus, beaker #3 is the correct choice. d) Na2SO4 is a soluble ionic compound and will fully dissociate into ions looking most like beaker #1.
-
Yes, because when CaCl2 dissociates it will form 3 ions (1 Ca2+ and 2 Cl– ions) whereas NaCl will only dissociate into 2 ions (Na+ and a Cl–) for each molecule. Thus, CaCl2 will generate more ions per mole than 1 mole of NaCl and be a better conductor of electricity.
-
If the amount of a substance required for a reaction is too small to be weighed accurately, the use of a solution of the substance, in which the solute is dispersed in a much larger mass of solvent, allows chemists to measure the quantity of the substance more accurately.
Numerical Problems
-
Calculate the number of grams of solute in 1.000 L of each solution.
- 0.2593 M NaBrO3
- 1.592 M KNO3
- 1.559 M acetic acid
- 0.943 M potassium iodate
-
Calculate the number of grams of solute in 1.000 L of each solution.
- 0.1065 M BaI2
- 1.135 M Na2SO4
- 1.428 M NH4Br
- 0.889 M sodium acetate
-
If all solutions contain the same solute, which solution contains the greater mass of solute?
- 1.40 L of a 0.334 M solution or 1.10 L of a 0.420 M solution
- 25.0 mL of a 0.134 M solution or 10.0 mL of a 0.295 M solution
- 250 mL of a 0.489 M solution or 150 mL of a 0.769 M solution
-
Complete the following table for 500 mL of solution.
Compound Mass (g) Moles Concentration (M) calcium sulfate 4.86 acetic acid 3.62 hydrogen iodide dihydrate 1.273 barium bromide 3.92 glucose 0.983 sodium acetate 2.42 -
What is the concentration of each species present in the following aqueous solutions?
- 0.489 mol of NiSO4 in 600 mL of solution
- 1.045 mol of magnesium bromide in 500 mL of solution
- 0.146 mol of glucose in 800 mL of solution
- 0.479 mol of CeCl3 in 700 mL of solution
-
What is the concentration of each species present in the following aqueous solutions?
- 0.324 mol of K2MoO4 in 250 mL of solution
- 0.528 mol of potassium formate in 300 mL of solution
- 0.477 mol of KClO3 in 900 mL of solution
- 0.378 mol of potassium iodide in 750 mL of solution
-
What is the molar concentration of each solution?
- 8.7 g of calcium bromide in 250 mL of solution
- 9.8 g of lithium sulfate in 300 mL of solution
- 12.4 g of sucrose (C12H22O11) in 750 mL of solution
- 14.2 g of iron(III) nitrate hexahydrate in 300 mL of solution
-
What is the molar concentration of each solution?
- 12.8 g of sodium hydrogen sulfate in 400 mL of solution
- 7.5 g of potassium hydrogen phosphate in 250 mL of solution
- 11.4 g of barium chloride in 350 mL of solution
- 4.3 g of tartaric acid (C4H6O6) in 250 mL of solution
-
Give the concentration of each reactant in the following equations, assuming 20.0 g of each and a solution volume of 250 mL for each reactant.
- BaCl2(aq) + Na2SO4(aq) →
- Ca(OH)2(aq) + H3PO4(aq) →
- Al(NO3)3(aq) + H2SO4(aq) →
- Pb(NO3)2(aq) + CuSO4(aq) →
- Al(CH3CO2)3(aq) + NaOH(aq) →
-
An experiment required 200.0 mL of a 0.330 M solution of Na2CrO4. A stock solution of Na2CrO4 containing 20.0% solute by mass with a density of 1.19 g/cm3 was used to prepare this solution. Describe how to prepare 200.0 mL of a 0.330 M solution of Na2CrO4 using the stock solution.
-
Calcium hypochlorite [Ca(OCl)2] is an effective disinfectant for clothing and bedding. If a solution has a Ca(OCl)2 concentration of 3.4 g per 100 mL of solution, what is the molarity of hypochlorite?
-
Phenol (C6H5OH) is often used as an antiseptic in mouthwashes and throat lozenges. If a mouthwash has a phenol concentration of 1.5 g per 100 mL of solution, what is the molarity of phenol?
-
If a tablet containing 100 mg of caffeine (C8H10N4O2) is dissolved in water to give 10.0 oz of solution, what is the molar concentration of caffeine in the solution?
-
A certain drug label carries instructions to add 10.0 mL of sterile water, stating that each milliliter of the resulting solution will contain 0.500 g of medication. If a patient has a prescribed dose of 900.0 mg, how many milliliters of the solution should be administered?
Answers
-
a. 39.13 g b. 161.0 g c. 93.57 g d. 201.8 g
-
a. 1.40 L of a 0.334 M solution, b. 25.0 mL of a 0.134 M solution, c. 150 mL of a 0.769 M solution
-
a. 0.815 M, b. 2.09 M, c. 0.182 M, d. 0.684 M
-
a. 0.174 M, b. 0.297 M, c. 0.048 M, d. 0.135 M
-
a. BaCl2 = 0.384 M, Na2SO4 = 0.563 M, b. Ca(OH)2 = 1.08 M, H3PO4 = 0.816 M, c. Al(NO3)3 = 0.376 M, H2SO4 = 0.816 M, d. Pb(NO3)2 = 0.242 M, CuSO4 = 0.501 M, e. Al(CH3CO2) = 0.392 M, NaOH = 2.00 M
-
0.48 M ClO−
-
1.74 × 10−3 M caffeine